SOLUTION: A circle of radius 3 is inscribed in ΔSPR. If SP = 7 and the altitude from R is 15, what is the sum of lengths of the other two sides of the triangle?

There can be no such triangle. It can be shown that the minimum altitude
from R which a triangle SPR can have with an inscribed circle of 
radius 3 and SP =7 is when such triangle SPR is isosceles.  And that
is when the altitude from R is 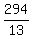 or 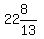.  So
no such triangle can have an altitude from R as short as 15, as your
problem states. 

The isosceles triangle SPR below is drawn to scale, with SP = 7,
and the inscribed circle has radius 3. Using similar right 
triangles OBR and PAR, it's easy to show that AR = .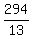
Thus altitude RA cannot possibly be as short as 15, `for this is
the minimum case.  You should point this out to your instructor.
There could have been a typo in one of the numbers.

 

Edwin