SOLUTION: Among all the pairs of numbers (x,y) such that 2x-y=12, find the pair for which the sum of the squares is a minimum. What is the minimum product?

Notice:  I changed your word "maximum" to "minimum".
That's because there is no maximum for either the sum of squares or
for the product.  Surely you must have meant "minumum".  Otherwise
there can be no solution, for the sum of the squares and the product
can both be millions, billions and trillions!  They can go to 
infinity!!!  Here is the problem for the minimums, not maximums.

Let S = the sum of the squares of x and y

(1) S = x²+y²
    
Solve 2x-y = 12 for y
        -y = -2x+12
         y = 2x-12

Substitute for y in (1)

   S = x² + (2x-12)²
   S = x² + (2x-12)(2x-12)
   S = x² + (4x²-48x+144)
   S = x² + 4x² - 48x + 144
   S = 5x² - 48x + 144
   
The graph of that is below.  Since we have already used y,
we have to use S, so think of the y-axis below as the S-axis.



From that graph you can see there can be no maximum.  However
there is a minimum at the vertex.

Using the vertex formula:

The x-coordinate of the vertex = 

The S-coordinate of the vertex is S = 5(4.8)² - 48(4.8) + 144 = 28.8

Now we must find y when x = 4.8

               y = 2(4.8)-12
               y = -2.4

So the pair (x,y) for which the sum of the squares is a minimum is (4.8,-2.4)

-------------------------------------------------------------------------
  
For the minimum product:

Let P = the product of x and y

(1) P = xy
    
We've already solved 2x-y = 12 for y
       
         y = 2x-12

Substitute for y in (1)

   P = x(2x-12)
   P = 2x²-12x

The graph of that is below.  Since we have already used y,
we have to use P, so think of the y-axis below as the P-axis.



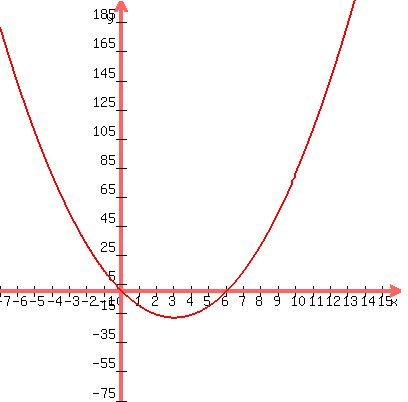Just as the other one, from that graph you can see there can 
be no maximum.  However there is a minimum at the vertex.

Using the vertex formula again:

The x-coordinate of the vertex = 

The P-coordinate of the vertex is P = 2(3)²-12(3) = -18

Now we must find y when x = 3

y = 2(3)-12
               y = -6

So the pair (x,y) for which the product is a minimum is (3,-6).

Edwin