Question 907484: Please help me solve this word problem: Joe is kayaking on a lake. He is 2 miles from the nearest point on the shoreline. From there he is 5 miles from his car. He can average 2 MPH kayaking and 3 MPH walking on the shore. He wishes to get to his car quicker so he heads to the shore at an angle towards his car.
There is a model using a right triangle with 2mi on the 90degree side. x is the length of the bottom and I don't know the hypotenuse length either. I need to find both x and the hypotenuse.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Joe's kayak is on the lake at point  (for KAYAK). (for KAYAK).
The nearest point on the shore is  (for NEAREST), (for NEAREST),
and Joe's car is next to the shoreline at point  (for CAR). (for CAR).
Joe will land the kayak at shoreline point  (for LANDING), (for LANDING),
which is somewhere between  and and  , ,
at a distance   from point from point  , ,
at a distance  (for hypotenuse) from point (for hypotenuse) from point  , ,
and at a distance 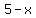 from point from point  . .

The Pythagorean theorem tells us that
 . .
The time (in hours) for Joe to cover that distance kayaking at 2 MPH is
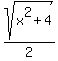 . .
The time (in hours) for Joe to cover the distance 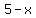 walkking at 3 MPH is walkking at 3 MPH is
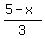
The total time (in hours for Joe to go from point  to point to point  is is

(  as a function of as a function of  ). ).
That much you would reason, regardless of your math class level and instructor preferences.
From this point on, what your instructor wants depends.
If you are being pushed to use and abuse a graphing calculator, you may be expected to graph the function 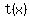 and find its minimum. and find its minimum.
If you are studying calculus, you may be expected to calculate the derivative of 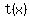 to find the point where the derivative is zero and to find the point where the derivative is zero and 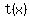 is minimum: is minimum:

 ---> --->  ---> --->  ---> --->  ---> --->  ---> --->  ---> --->  ---> ---> 
So  . .
(Joe should aim for landing  miles from point miles from point  . .
Now that we have found  for Joe, for Joe,
he has all the side lengths for right triangles  (pictured) and (pictured) and 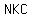 (imagine it), (imagine it),
so I would let Joe figure out the angles 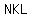 , , 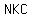 and and 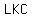
that he can use to get going in the right direction.
|
|
|