Question 907313: A rectangular storage container with an open top is to have a volume of 10 m3. The length of this base is twice the width. Material for the base costs $20 per square meter. Material for the sides costs $12 per square meter. Find the cost of materials for the cheapest such container. (Round your answer to the nearest cent.)
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! x for length, y for width,
x=2y
volume is 10 cubic meters, so if for z height,
xyz=10
Finding z:
Still more information is needed to have a better relationship among the three dimensions.
These are the costs of the different rectangular parts altogether:
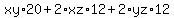
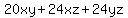
and if you substitute for y,
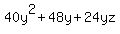 -----This cost written in terms of y and z.
You can use the earlier found, to either substitute for y or for z in the cost function.
First, simplify the "10" equation to  .
 ; substitute for z, done here.
cost,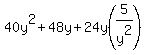 
 .
This is probably meant as a calculus problem using the derivative  .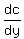
Form the derivative, and solve for y in  to find and check extremes (for a minimum value for c).
|
|
|
