|
Question 90671: Find all real zeros of the function:
* f(x)=x^4-16x^2+15
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Any rational zero can be found through this equation
 where p and q are the factors of the last and first coefficients where p and q are the factors of the last and first coefficients
So let's list the factors of 15:

Now let's list the factors of 1:

Now let's divide each factor of the last coefficient by each factor of the first coefficient

Now simplify
These are all the possible zeros of the function

To save time, I'm only going to use synthetic division on the possible zeros that are actually zeros of the function.
Otherwise, I would have to use synthetic division on every possible root (there are 8 possible roots, so that means there would be at most 8 synthetic division tables).
However, you might be required to follow this procedure, so this is why I'm showing you how to set up a problem like this
If you're not required to follow this procedure, simply use a graphing calculator to find the roots
So with a graphing calculator, we find one root at x=-1
so our test zero is -1
Now set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the numerator to the right of the test zero.(note: remember if a polynomial goes from  to to 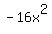 there is a zero coefficient for there is a zero coefficient for  . This is simply because . This is simply because 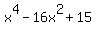 really looks like really looks like 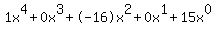
Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 1)
Multiply -1 by 1 and place the product (which is -1) right underneath the second coefficient (which is 0)
Add -1 and 0 to get -1. Place the sum right underneath -1.
Multiply -1 by -1 and place the product (which is 1) right underneath the third coefficient (which is -16)
Add 1 and -16 to get -15. Place the sum right underneath 1.
Multiply -1 by -15 and place the product (which is 15) right underneath the fourth coefficient (which is 0)
Add 15 and 0 to get 15. Place the sum right underneath 15.
| -1 | | | 1 | 0 | -16 | 0 | 15 | | | | | -1 | 1 | 15 | | | | | 1 | -1 | -15 | 15 | |
Multiply -1 by 15 and place the product (which is -15) right underneath the fifth coefficient (which is 15)
| -1 | | | 1 | 0 | -16 | 0 | 15 | | | | | -1 | 1 | 15 | -15 | | | | 1 | -1 | -15 | 15 | |
Add -15 and 15 to get 0. Place the sum right underneath -15.
| -1 | | | 1 | 0 | -16 | 0 | 15 | | | | | -1 | 1 | 15 | -15 | | | | 1 | -1 | -15 | 15 | 0 |
Since the last column adds to zero, we have a remainder of zero. This means  is a factor of is a factor of 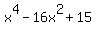
Now lets look at the bottom row of coefficients:
The first 4 coefficients (1,-1,-15,15) form the quotient
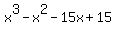
So 
You can use this online polynomial division calculator to check your work
Using the same technique above, we find another zero at x=1
Now lets perform synthetic division on 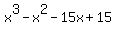 with the test zero of x=1 with the test zero of x=1
Now set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the numerator to the right of the test zero.
Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 1)
Multiply 1 by 1 and place the product (which is 1) right underneath the second coefficient (which is -1)
Add 1 and -1 to get 0. Place the sum right underneath 1.
Multiply 1 by 0 and place the product (which is 0) right underneath the third coefficient (which is -15)
Add 0 and -15 to get -15. Place the sum right underneath 0.
Multiply 1 by -15 and place the product (which is -15) right underneath the fourth coefficient (which is 15)
Add -15 and 15 to get 0. Place the sum right underneath -15.
Since the last column adds to zero, we have a remainder of zero. This means  is a factor of is a factor of 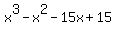
Now lets look at the bottom row of coefficients:
The first 3 coefficients (1,0,-15) form the quotient
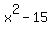
So 
You can use this online polynomial division calculator to check your work
Now set 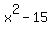 equal to zero equal to zero


 Take the square root of both sides Take the square root of both sides
So two roots are
 or or 
---------------------------------
Answer:
So the roots are  , ,  , ,  or or 
|
|
|
| |