Question 906226: Graph the inequality. y < 1/3x +2 (Please clearly label the points when you graph it so I can see how you got the answer.) Thanks :)
*I do know that it is a dashed line because it's a <(greater than symbol)
* I also know that if it's false, the other side is shaded. And if it's true, you shade the side with the test point.
Thanks for the help :)
Found 2 solutions by josgarithmetic, Theo:
Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website! You have a strict inequality, based on the line  , so instead of darkening the line, you EXCLUDE it (because you have 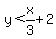 , not the equation), and you shade the region below the line. On paper, you would show a dotted line for the reference equation, not a solid line. As YOU described, you have no misunderstanding, so what help you need seems not to be any.
You specifically request to have the points LABELED when it is graphed. The solution to the inequality IS NOT A POINT. The solution is a REGION BELOW AND EXCLUDING the reference line. You need to understand that you are not missing anything and need to recognize that you are not missing anything. We do not label the solution points; we SHADE the solution region.
The line is supposed to be dotted, not solid, although you may be unable to distinguish if it appears dotted or not, but the code for this graph IS entered as a strict inequality.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! you graph y = 1/3x + 2.
this gets you your line.
you draw the line as dashed because your solution will be under the line and not on it.
this is because the equation says < rather than <=.
the area that you shade will be under the line.
it's the area that makes the equation true.
your test, if you need to make it, is at a specific value of x.
since your equation states that y < 1/3x + 2, than any value of y that you choose at that value of x must be less than the corresponding value of y at that value of x that is on the line.
for example:
you choose x = 6
when x = 6, the equation of y = 1/3x + 2 becomes y = 1/3*6 + 2 which makes y = 4.
any value of y < 4 when x = 6 will satisfy the equation.
any value of y >= 4 when x = 6 will not satisfy the equation.
the graph of your equation is shown below:
|
|
|
