Question 906208: a random sample of 88 observations produced a mean x = 25.8 and standard deviation s=2.7. Find 95%, 90% and 99% confidence interval for u
I have been trying to figure out how to do this problem for hours but I keep getting stuck. If someone can show me step by step it would help me alot. Thank you so much.
Found 2 solutions by ewatrrr, Theo:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! sample size = 88
mean = 25.8
standard deviation = 2.7
mu or what you show as u is presumably the mean of the population that this sample was taken from.
if my assumption is correct, then you would solve this as follows:
standard error, which is the standard deviation of the distribution of sample means, is equal to standard deviation divided by the square root of the sample size.
this makes se = 2.7 / sqrt(88) which makes se = .29 rounded to 2 decimal places which should be adequate for the accuracy that you need, and certainly enough to show you the concept of what you're trying to do.
se represents standard error.
sqrt represents square root of.
you want to find the interval where the population mean is expected to be within 95% of the time, 90% of the time, and 99% of the time.
you will want to find the z-scores that correspond to those confidence limits.
x-scores and x-factors mean the same thing. i sometimes use z-scores and i sometimes use z-factors but i'm talking about the same thing.
a two sided confidence interval is assumed.
that means that the interval will have a tail at both ends that is outside the confidence interval.
this is standard procedure unless indicated otherwise.
for a 95% confidence interval, the tail will be calculated as (100%-95%)/2 = 2.5% of the area at each end.
for a 90% confidence interval, you will have a tail of 5% at each end.
for a 99% confidence interval, you will have a tail of .5% at each end.
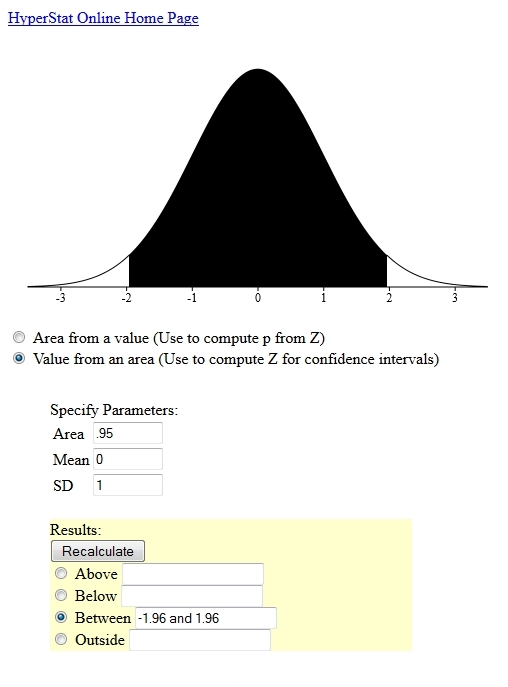
at 95%, you look for an area of 97.5% which is an area of .975 which will generate a z-factor of 1.96.
at 90%, you will look for an area of 95% which is an area of .95 which will generate a z-factor of 1.65.
at 99%, you will look for an area of 99.5% which is an area of .995 which will generate a z-factor of 2.58
all z factors have been rounded to 2 decimal places.
you now want to find the limits of your sample mean where you expect the population mean to be within 95% of the time, 90% of the time, or 99% of the time.
to find the margin of error, you multiply the limiting z factor * the standard error.
the limiting z-factor is also called the critical z-factor.
at 95% confidence interval, your margin of error will be plus or minus 1.96 * .29 which is equal to plus or minus .57 rounded to 2 decimal places.
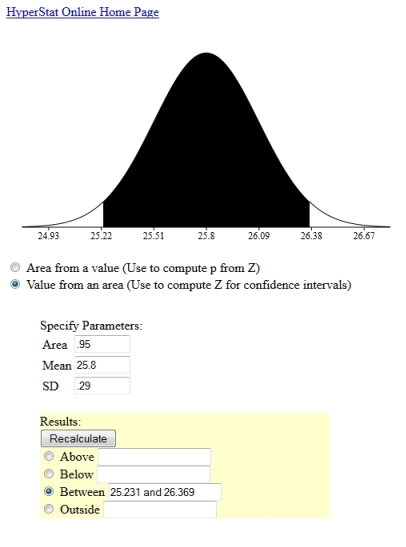
since your sample mean is 25.8, then your 95% confidence interval based on that sample mean is 25.8 - .57 to 25.8 + .57.
this results in an interval from 25.23 to 26.37
you will be 95% confident that your population mean is within the interval of from 25.23 to 26.37 based on this sample.
you can do the same calculations using the critical z-factors for 90% confidence interval and 99% confidence interval.
what will change is the margin of error.
the higher the confidence level, the greater is the margin of error.
the formula for margin of error is standard error * critical z-factor.
at 90% confidence interval, the margin of error will be 25.8 plus or minus .29 * 1.65.
at 99% confidence interval, the margin of error will be 25.8 plus or minus .29 * 2.58
hopefully you can do the rest from here.
if not, let me know and i'll guide you further depending on what your questions are.
a picture of what i just calculated for you will look like this from the z-score perspective:
a pictures of what i just calculated for you will look like this from the mean and standard error perspective:
|
|
|