SOLUTION: How to solve inequalities with two absolute value. Is there any easy way? Kindly help me. Here's the question! Solve the inequality {{{1 - abs(x+1) > abs(2x-1) }}}.

Algebra ->  Absolute-value -> SOLUTION: How to solve inequalities with two absolute value. Is there any easy way? Kindly help me. Here's the question! Solve the inequality {{{1 - abs(x+1) > abs(2x-1) }}}.      Log On


   

Question 906047: How to solve inequalities with two absolute value. Is there any easy way? Kindly help me. Here's the question!
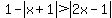Solve the inequality 1+-+abs%28x%2B1%29+%3E+abs%282x-1%29+.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Each absolute value expression has two possible cases. The expression inside is nonnegative or it is negative. Evaluate each case. Your inequality statement has two absolute values, so there are FOUR cases to check.

CASE x%2B1%3E=0 and 2x-1%3E=0

CASE x%2B1%3C0 and 2x-1%3E=0

CASE x%2B1%3E=0 and 2x-1%3C0

CASE x%2B1%3C0 and 2x-1%3C0

Can you make the simplifications to the inequality for each case and solve for it?

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
How to solve inequalities with two absolute value. Is there any easy way? Kindly help me. Here's the question!
Solve the inequality 1+-+abs%28x%2B1%29+%3E+abs%282x-1%29+.


In most cases, you have to examine the absolute inequality. That's the easiest way.



Observing the absolute inequality, the ONLY time the left side is POSITIVE is when x = - 1. 

As a result, the right side would equal 3. Thus, the INEQUALITY will be false, as 1 IS NOT > 3. 



Additionally, the left side is zero (0), when x = 0, and x = - 2. As a result, the right side

would equal 1 and 5, respectively. Thus, the INEQUALITY will be false, as 0 IS NEITHER > 1, NOR > 5. 



Any other value for x makes the left-side NEGATIVE, while the right side will always be POSITIVE. 



Therefore, NO SOLUTION exists for this absolute inequality.



You could have also subtracted 1 to get: 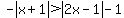-+abs%28x+%2B+1%29+%3E+abs%282x+-+1%29+-+1. It's clear from this that the left side's GREATEST

value (0) occurs when x = - 1, which makes the right side, 2, and the inequality, FALSE. All other values for x

would result in the left side value being negative, or < 0.