Question 905669: Please classify each system and determine the number of solutions.
1.) 7x+y=13 and 28x+4y=-2
2.) 2x-3y=-15 and 3y-2x=15
3.) 8y-24x=64 and 9y+45x=72
4.) 2x+2y=-10 and 4x+4y=-16
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1.)
 and and

| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Subtract Subtract 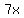 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 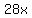 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines are parallel and will never intersect. So there are no solutions and the system is inconsistent. |
2.)
 and and

| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Subtract Subtract 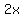 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
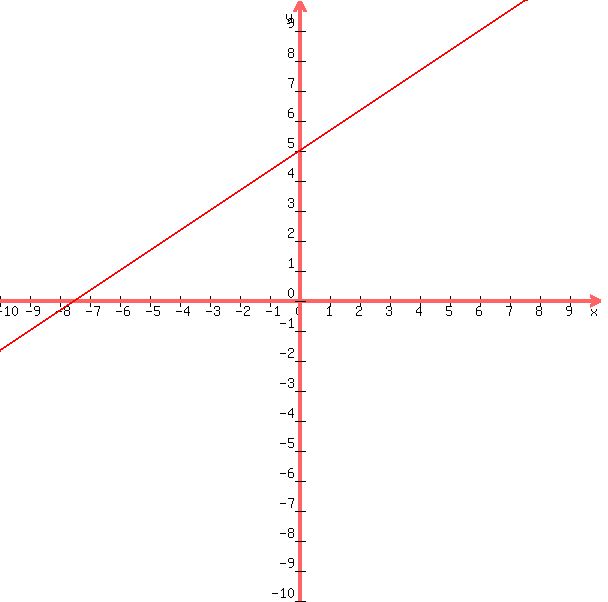 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Add Add 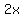 to both sides to both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines are identical (one lies perfectly on top of the other) and intersect at all points of both lines. So there are an infinite number of solutions and the system is dependent. |
3.)
 and and

or
 and and

| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Add Add 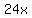 to both sides to both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
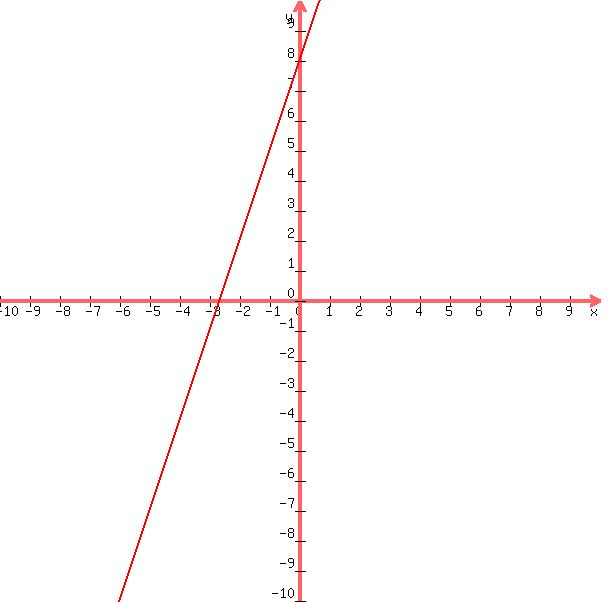 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 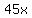 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines intersect at the point ( , , ) (note: you might have to adjust the window to see the intersection) ) (note: you might have to adjust the window to see the intersection) |
4.)
 and and

| Solved by pluggable solver: Solve the System of Equations by Graphing |
Start with the given system of equations:


In order to graph these equations, we need to solve for y for each equation.
So let's solve for y on the first equation
 Start with the given equation Start with the given equation
 Subtract Subtract 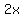 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets graph  (note: if you need help with graphing, check out this solver) (note: if you need help with graphing, check out this solver)
 Graph of Graph of 
So let's solve for y on the second equation
 Start with the given equation Start with the given equation
 Subtract Subtract 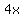 from both sides from both sides
 Rearrange the equation Rearrange the equation
 Divide both sides by Divide both sides by 
 Break up the fraction Break up the fraction
 Reduce Reduce
Now lets add the graph of  to our first plot to get: to our first plot to get:
 Graph of Graph of  (red) and (red) and  (green) (green)
From the graph, we can see that the two lines are parallel and will never intersect. So there are no solutions and the system is inconsistent. |
|
|
|