Question 90564: Hi, how do i perform the following operation and express it in standard form?
2 - 6i / 4 - 9i
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! The discussion shows one of a couple of ways that you can do this problem.
.
This way involves converting the denominator to a real number and then dividing that real
number into each of the terms in the resulting complex numerator.
.
Suppose we find the complex conjugate of the denominator. Since the denominator is 4 - 9i, its
complex conjugate is the same but with the opposite sign between it real and imaginary
parts. In other words, the complex conjugate of the denominator is 4 + 9i.
.
Now suppose we multiply the original problem by:
.
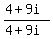
.
Notice that this fraction, composed of the complex conjugate over the complex conjugate
is equivalent to 1, so in effect we are multiplying the original problem by 1. This multiplication
is written as:
.

.
Notice that the multiplication of the denominators involves two terms of the form
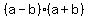 . If you multiply out this form the answer you get is . If you multiply out this form the answer you get is 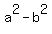
a form that you might recall from basic algebra. In this problem a = 4 and b = 9i, so the
multiplication of the two denominators results in 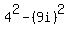 . Squaring the 4 . Squaring the 4
results in 16 and squaring the 9i results in 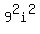 . But recall that the definition . But recall that the definition
of  is that it equals -1. So when you square 9i you get 81*(-1) or -81. So the product is that it equals -1. So when you square 9i you get 81*(-1) or -81. So the product
of the denominator of the original problem times its conjugate ... in other words 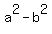
becomes 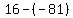 which is which is  . Let's not lose sight of what is . Let's not lose sight of what is
going on here. So far what we have done has resulted in:
.

.
Observe that the resulting denominator is a real number ... it is 97. Now we need to
multiply 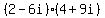 . First multiply the 2 times (4 + 9i) to get 8 + 18i. Then . First multiply the 2 times (4 + 9i) to get 8 + 18i. Then
multiply the -6i times (4 + 9i) to get 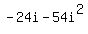 . Then combine the two products . Then combine the two products
to get:
.
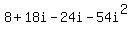
.
The +18i and the - 24i combine to give -6i, simplifying the result to:
.
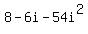
.
Again, recall that the definition of  is that is that  . Substituting . Substituting
-1 for  results in: results in:
.

.
So the problem progression is now:
.

.
As a final step, all that needs to be done now is to divide 97 into each of the terms of
the numerator and the answer becomes:
.

.
And there's the answer.
.
Hope this helps you to understand the problem. It's important to know that if you have a
complex denominator, you can convert it to a real number by multiplying it by its
conjugate ... but when you do that multiplication, you must also multiply the numerator
by that same conjugate. The rest of the problem involves just careful multiplication
and the recognition that  . .
.
|
|
|