|
Question 905545: I have a question from a worksheet that is confusing to me:
Explain in words how to write an equation that is part one: parallel and then also part two: perpendicular to the equation y=2/3x-4 passing through the point (-2,-5). Write your answer in standard form.
I'm hoping to get a detailed answer so I know what I'm doing on the test next week... Thanks in advance!
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! write an equation that is part one: parallel and then also part two: perpendicular to the equation y=2/3x-4 passing through the point (-2,-5). Write your answer in standard form.
:
y =  x - 4
equations of parallel lines have the same slope
Using the slope intercept form y = mx + b
Replace x and y with the given point, x=-2; then y = -5, slope is 2/3
-5 = (-2) + b
-5 =  + b
-5 +  = b
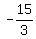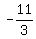 + = b
 = b
the equation
y = x -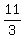 
The standard form ax + by = c, with all integer coefficients
Multiply our equation by 3 to get rid of the denominators
3y = 2x - 11
-2x + 3y = -11
or you can mult by -1 and you have fewer negatives
2x - 3y = 11
:
perpendicular, the slopes relationship; m1*m2 = -1
Assuming m1 = 2/3, find m2
* m2 = -1
Multiply both sides by 3/2 and you have
m2 =  Using the slope intercept form y = mx + b
Replace x and y with the given point, x=-2; then y = -5, slope is -3/2
-5 = (-2) + b
-5 = 3 + b
-5 - 3 = b
b = -8
the equation
y = x - 8
The standard form ax + by = c, with all integer coefficients
Multiply our equation by 2 to get rid of the denominators
2y = -3x - 16
3x + 2y = -16 is the standard form
:
You can check this for yourself replace x with -2 and y with -5, equals -16
|
|
|
| |
