log(6x-3)base 3=1+log(x-3)base3)
What the other person who responded, says (see below), is TOTALLY FALSE!! His/Her answer is also WRONG, so IGNORE it all!!
WRONG!! WRONG!! WRONG!!
Since the bases of the logs are the same (number 3 in this case), then the insides must be equal. That is:
6x - 3 = 1 + x - 3
6x - x = 3 - 3 + 1
5x = 1
x = 1/5
Understand?
 Notice that there is a 1 ATTACHED to the log on the right!
Anyway, the smaller variable-expression, x - 3, MUST be > 0. We then get: x - 3 > 0, and x > 3. The problem then becomes:
Notice that there is a 1 ATTACHED to the log on the right!
Anyway, the smaller variable-expression, x - 3, MUST be > 0. We then get: x - 3 > 0, and x > 3. The problem then becomes:
 , with the constraint, x > 3.
, with the constraint, x > 3.

 ---- Applying
---- Applying 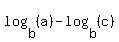 =
= 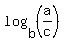
 --- Converting to EXPONENTIAL form
6x - 3 = 3(x - 3) ----- Cross-multiplying
6x - 3 = 3x - 9
6x - 3x = - 9 + 3
3x = - 6
--- Converting to EXPONENTIAL form
6x - 3 = 3(x - 3) ----- Cross-multiplying
6x - 3 = 3x - 9
6x - 3x = - 9 + 3
3x = - 6
 However, x = - 2 is NOT a solution, as it is NOT > 3, which makes this x-value, EXTRANEOUS!. So, there are NO SOLUTIONS!
However, x = - 2 is NOT a solution, as it is NOT > 3, which makes this x-value, EXTRANEOUS!. So, there are NO SOLUTIONS!