Question 90501: Please help me solve my assignment. Thank you.
Two planes take off from an airport at 9:15 AM. One flies on a course of 86 deg. at a constant rate of 190 mi/h.The second one flies on a course of 176 deg. at 160 mi/h. How far apart are they at 10:45 AM?
Found 2 solutions by kev82, Earlsdon:
Answer by kev82(151)   (Show Source): (Show Source):
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! The two planes leave from the same airport at 9:15 am.
One flies a course of 86 degrees (from north) at 190 mph.
The other flies a course of 176 degrees at 160 mph.
Now if you draw a diagram of this situation, place a point representing the airport and draw two lines representing the paths of the two airplanes.
The first line will be drawn at an angle of 86 degrees (clockwise) from north while the second line will be drawn at an angle of 179 degrees (clockwise) from north.
You will notice one thing right away, the two line make a 90-degree angle between them. 176 degrees - 86 degrees = 90 degrees.
Now, if you knew the length of each line you could use the Pythagorean Theorem to solve the problem.
The length of each line (path) represents the distance traveled by each plane during the time between 9:15 am and 10:45 am. Well, this is just 1.5 hours.
To find the distance, use d = rt, or distance = rate(speed) times time (1.5 hours)
So, for the first plane, the distance traveled is: d = (190 mph)(1.5 hrs) = 285 miles.
For the second plane, d = (160 mph)(1.5 hrs) = 240 miles.
To find their distance from each other (D) at 10:45 am, you want to find the length of the hypotenuse of the right triangle, so...
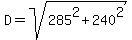


 miles. miles.
The distance between the two planes at 10:45 am is 372.6 miles.
|
|
|