SOLUTION: if an orange is tossed upward from a height of 13 feet at an initial velocity of 18 feet per second, then its height h after t seconds is given by the function h(t)= -16t^2+18t+13,

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: if an orange is tossed upward from a height of 13 feet at an initial velocity of 18 feet per second, then its height h after t seconds is given by the function h(t)= -16t^2+18t+13,      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 904309: if an orange is tossed upward from a height of 13 feet at an initial velocity of 18 feet per second, then its height h after t seconds is given by the function h(t)= -16t^2+18t+13, where h is in feet.
A. How long will the object be in the air before it hits the ground?
b. How long will it take to reach 4 feet?
Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
A) set h(t) to 0 and solve
0= -16t^2+18t+13
Solved by pluggable solver: Quadratic Formula
Let's use the quadratic formula to solve for t:


Starting with the general quadratic


at%5E2%2Bbt%2Bc=0


the general solution using the quadratic equation is:


t+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29




So lets solve -16%2At%5E2%2B18%2At%2B13=0 ( notice a=-16, b=18, and c=13)





t+=+%28-18+%2B-+sqrt%28+%2818%29%5E2-4%2A-16%2A13+%29%29%2F%282%2A-16%29 Plug in a=-16, b=18, and c=13




t+=+%28-18+%2B-+sqrt%28+324-4%2A-16%2A13+%29%29%2F%282%2A-16%29 Square 18 to get 324




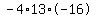t+=+%28-18+%2B-+sqrt%28+324%2B832+%29%29%2F%282%2A-16%29 Multiply -4%2A13%2A-16 to get 832




t+=+%28-18+%2B-+sqrt%28+1156+%29%29%2F%282%2A-16%29 Combine like terms in the radicand (everything under the square root)




t+=+%28-18+%2B-+34%29%2F%282%2A-16%29 Simplify the square root (note: If you need help with simplifying the square root, check out this solver)




t+=+%28-18+%2B-+34%29%2F-32 Multiply 2 and -16 to get -32


So now the expression breaks down into two parts


t+=+%28-18+%2B+34%29%2F-32 or t+=+%28-18+-+34%29%2F-32


Lets look at the first part:


x=%28-18+%2B+34%29%2F-32


t=16%2F-32 Add the terms in the numerator

t=-1%2F2 Divide


So one answer is

t=-1%2F2




Now lets look at the second part:


x=%28-18+-+34%29%2F-32


t=-52%2F-32 Subtract the terms in the numerator

t=13%2F8 Divide


So another answer is

t=13%2F8


So our solutions are:

t=-1%2F2 or t=13%2F8


t = 13/8
B) set h(t) to 4 and solve
4= -16t^2+18t+13
t=3/2
Solved by pluggable solver: Quadratic Formula
Let's use the quadratic formula to solve for t:


Starting with the general quadratic


at%5E2%2Bbt%2Bc=0


the general solution using the quadratic equation is:


t+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29




So lets solve -16%2At%5E2%2B18%2At%2B9=0 ( notice a=-16, b=18, and c=9)





t+=+%28-18+%2B-+sqrt%28+%2818%29%5E2-4%2A-16%2A9+%29%29%2F%282%2A-16%29 Plug in a=-16, b=18, and c=9




t+=+%28-18+%2B-+sqrt%28+324-4%2A-16%2A9+%29%29%2F%282%2A-16%29 Square 18 to get 324




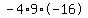t+=+%28-18+%2B-+sqrt%28+324%2B576+%29%29%2F%282%2A-16%29 Multiply -4%2A9%2A-16 to get 576




t+=+%28-18+%2B-+sqrt%28+900+%29%29%2F%282%2A-16%29 Combine like terms in the radicand (everything under the square root)




t+=+%28-18+%2B-+30%29%2F%282%2A-16%29 Simplify the square root (note: If you need help with simplifying the square root, check out this solver)




t+=+%28-18+%2B-+30%29%2F-32 Multiply 2 and -16 to get -32


So now the expression breaks down into two parts


t+=+%28-18+%2B+30%29%2F-32 or t+=+%28-18+-+30%29%2F-32


Lets look at the first part:


x=%28-18+%2B+30%29%2F-32


t=12%2F-32 Add the terms in the numerator

t=-3%2F8 Divide


So one answer is

t=-3%2F8




Now lets look at the second part:


x=%28-18+-+30%29%2F-32


t=-48%2F-32 Subtract the terms in the numerator

t=3%2F2 Divide


So another answer is

t=3%2F2


So our solutions are:

t=-3%2F8 or t=3%2F2