Question 903823: How do I factor this?
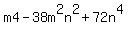
The answer is 
I'm confused on how they got this answer. The 38 is not a typo, either.
Found 3 solutions by jim_thompson5910, josgarithmetic, MathTherapy:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! Not remembering any instruction during Introductory Algebra from so long ago that dealt with factoring degree 4 trinomial, eventually further instruction combined from Introductory and College Algebra contained enough knowledge to use polynomial division for trying to handle something like you have; including Rational Roots Theorem, although you are not interested in roots here.
There is m^4 and n^4, the n^4 term having coefficient 72. Factors of 72 are 2, 3, 6, 12, 24,36.
You would want to test DIVISORS of  , , 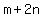 , ,  , , 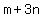 , , 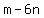 , , 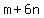 , ... possibly others. Your DIVIDEND must be formed as , ... possibly others. Your DIVIDEND must be formed as 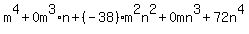 ; ;
After finding the quotient with remainder of zero, you next use whatever skills you have for factoring, or you might try another polynomial division on the quotient, choosing a divisor that you believe is worth testing.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|