Question 90369: Suppose you wanted to construct a fence around a garden plot in the form of a rectangle. On the neighbor’s side it’s going to need heavy-duty fencing that costs $2.00 per foot. The other three sides can be made of standard fencing material that costs $1.20 foot. You have $200 to spend.
1. How many different rectangles would it be possible to enclose for $200?
2. Write an equation using two variables for the total cost of the fence. Use x and y to represent the width and length of the rectangle. Solve the equation for one of the variables (either x or y).
3. Given that Area = (x)(y), now write the area function for this problem using ONLY ONE VARIABLE (by making a substitution using the equation from #2).
4. What dimensions will give the maximum area inside the fence?
5. What will be the maximum area?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.
First draw the picture. In this drawing the thicker line at the top denotes the neighbor's side (which is denoted as N)

Notice the length of W is equal to N
So the perimeter of this rectangle is

And the cost function is

Now since N=W, we can replace N with W
 replace N with W replace N with W
 Combine like terms Combine like terms
 Multiply 1.2 and 2L to get 2.4L Multiply 1.2 and 2L to get 2.4L
Also, since you have at most is $200, this means the cost of the fence must be less than $200. So we have this inequality
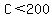
Now replace C with 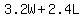
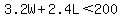
Now lets solve for L
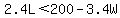 Subtract 3.4W from both sides Subtract 3.4W from both sides
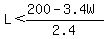 Divide both sides by 2.4 Divide both sides by 2.4
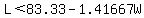 Divide Divide
Now since we don't know the value of W, we cannot solve for L. Since there are two unknown variables, there are an infinite number of possible rectangles. For instance, the neighbor's side might be 10 feet
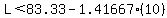 plug in w=10 plug in w=10
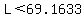 evaluate evaluate
So in this case there are 69 possible rectangles (if the length is a whole number)
or
the neighbor's side might be 20 feet
 plug in w=20 plug in w=20
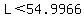 evaluate evaluate
So in this case there are 53 possible rectangles (if the length is a whole number)
If the length can be any decimal number, then there are an infinite number of rectangles
This list goes on...
So this means we cannot figure out how many possible combinations of rectangles we can make. So I would double check your problem. If that is the correct info, then there's a strong chance that there are an infinite number of rectangles.
------------------------------------------------------------------------
2.
We previously solved for the cost function

Just replace W and L with x and y

Now lets solve for y
 Start with the cost function Start with the cost function
 Subtract 3.2x from both sides Subtract 3.2x from both sides
 Divide both sides by 2.4 Divide both sides by 2.4
So we get

------------------------------------------------------------------------
3.
Area:

Using our previous answer, plug in  into into 

 Distribute Distribute
Since the cost must be what we have in our pocket, the cost is 200. So c=200
 Plug in c=200 Plug in c=200
------------------------------------------------------------------------
4.
If we plot  as a function of x, we get as a function of x, we get
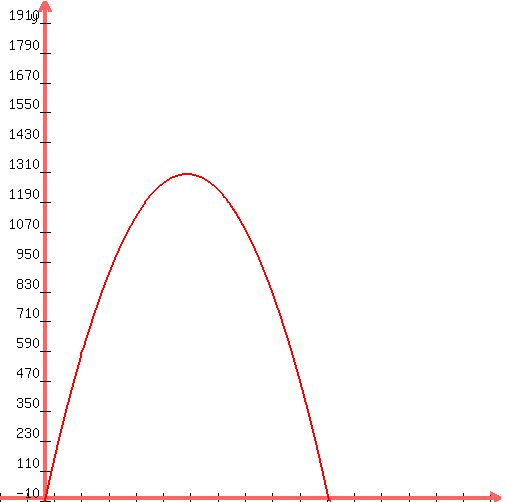
Notice how the graph peaks at a certain value. At this x-value, this x-value is one dimension which forms the maximum area.
So using a calculator, we get x=41.667
This means that the maximum area is formed when one dimension is 41.667
Now plug in x=41.667 into  to find the other dimension to find the other dimension

And with a calculator we get

So the maximum area is formed when  and and 
------------------------------------------------------------------------
5.
Now plug in  and and  into into 


So the maximum area is 1,157.384259 square feet
|
|
|