Question 90319: The problem says factor:
x^2-25
x^2-7x-12
I forgot how to factor these so maybe if you just explain it briefly I might remember,thank you.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ah yes...factoring!!
1) Factor:
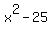 Look at each term and notice that they are both "perfect squares". Look at each term and notice that they are both "perfect squares".
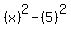
This suggests that the factors will be of the form:
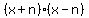 which would get you which would get you 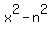 when multiplied. when multiplied.
So, in this case, n = 5 so the factors are:

2) Factor:
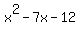
The factors will have the form: 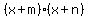 where: where:
 and and

The two numbers come to mind are 3 and 4 becuase:
 and and

Now all you have to do is to make sure the signs of the two numbers, n and m, will give the correct signs (negative, in this case) for the sum and the product.
But, there is a problem!
To get a product of -12, the 3 and the 4 must have opposite signs, right?
But if the 3 and the 4 have opposite signs, then their sum can never be -7, can it?
So, scrap the 3 and the 4.
What other factors of 12 are there?
-1*12 or 1*-12
-2*6 or 2*-6
Looking at these factors, there's no way you are going to get a sum -7
So, you have to say that:
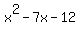 is prime! (Not factorable) is prime! (Not factorable)
Now if your expression had been:
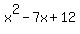 then you could factor this as: then you could factor this as:

But it isn't, so you can't!
|
|
|