Question 903078: Is the average of 5consecutive even numbers equal to the average of 5 consecutive odd numbers.
Found 2 solutions by Edwin McCravy, solver91311:
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website!
Let the five consecutive even integers be
2n, 2n+2, 2n+4, 2n+6, 2n+8
Let the five consecutive odd integers be
2k+1, 2k+3, 2k+5, 2k+7, 2k+9.
Assume, for contradiction, that their averages can be equal
If their averages are equal, then
  
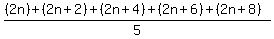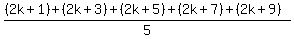Multiply both sides by 5
 
 
 
 
 
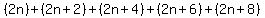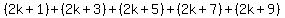
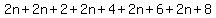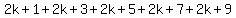
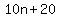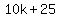
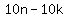
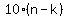
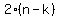This cannot be, because the left side
is even and the right side is odd.
This is a contradiction.
Therefore the answer is "NO", the average of 5 even integers
can never be equal to the average of 5 odd integers.
Edwin
Answer by solver91311(24713)  (Show Source):
You can put this solution on YOUR website!
No.
Let  represent an arbitrary even integer. Then  is the next consecutive even integer.  is the next after that, and so on. The sum of five consecutive even integers is then  , and the average is then that sum divided by 5, namely .
Similarly, if  is an arbitrary odd integer, the sum of five consecutive odd integers would be  and the average would be  .
In order for there to be a set of five consecutive even integers that have an average equal to the average of a set of five consecutive odd integers, then the statement:
must be true and therefore
must be true.
Since there is no even integer that is equal to an odd integer, this relation can never be true. Hence, a set of 5 consecutive even integers whose average is equal to the average of a set of 5 consecutive odd integers does not exist.
John
My calculator said it, I believe it, that settles it
|
|
|
