Question 902623: When a polynomial P(x) is divided by x + 3 , the remainder is 2. Which point must be on the
graph of the corresponding function y = P(x).
Please show the steps and explain. I just can't figure this one out!
Your help is TRULY appreciated, thanks you thank you thank you!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if f(a) = r, then the point (a,r) must be on the graph of the equation.
when you divide an equation by x - a, then this is the same as finding f(a) with r being the remainder of the division.
if you divide the polynomial by x+3, this is the same as finding f(-3) and the result of that will be the remainder of 2.
this means that the point (-3,2) must be on the graph.
an example will show you what i mean.
assume the equation is x^2 + x - 4
if you divide that equation by x+3, you will get 2 as a remainder.
if you evaluate f(x) = x^2 + x - 4 at f(-3), you will get (-3)^2 - 3 - 4 = 9 - 7 = 2
the point (-3,2) must be on the graph of the equation.
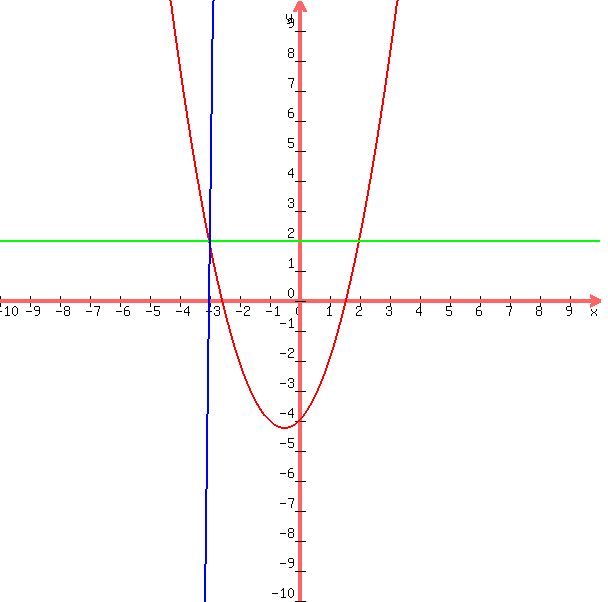
you can see if that's true by graphing x^2 + x - 4 and x = -3 and y = 2 and see if they intersect on the graph of that equation.
the graph looks like this:
the intersection of the vertical line at x = -3 and the horizontal line at y = 2 with the graph of the equation x^2 + x - 4 is at the point (-3,2).
this is all part of the remainder theorem which you can read at the following link.
http://www.purplemath.com/modules/remaindr.htm
|
|
|