|
Question 902237: Solve the absolute value inequality. Express the answer using interval notation.
7 − |2x + 3| ≤ 6
Must graph the solution set. Please explain how to solve. Thank You!
Found 2 solutions by stanbon, Theo:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve the absolute value inequality. Express the answer using interval notation.
7 − |2x + 3| ≤ 6
Must graph the solution set. Please explain how to solve. Thank You!
------
Graph the left side and the right side separately, but on the same
x/y coordinate system.
-------

-----
Ans: Find the interval on the x-axis where the left side
is <= the right side::
--------
Cheers,
Stan H.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! start with 7 - abs(2x+3) <= 6
subtract 7 from both sides of the equation to get:
- abs(2x+3) <= -1
multiply both sides of this equation by -1 to get:
abs(2x+3) >= 1
when 2x+3 >= 0, this equation becomes:
2x+3 >= 1
solve for x to get x >= -1
when 2x+3 < 0, this equation becomes:
2x+3 <= -1
solve for x to get x <= -2
your solutions are:
x >= -1 or x <= -2
in interval notation this solution is:
(-infinity,-2] or [-1,infinity)
you would graph this equation as follows:
start with abs(2x+3) >= 1
graph y = abs(2x+3) and graph y = 1 on the same graph.
your solution lies in the region where the graph of y = abs(2x+3) is greater than or equal to the graph of y = 1.
that occurs when x <= -2 and when x >= -1.
that graph is shown below:
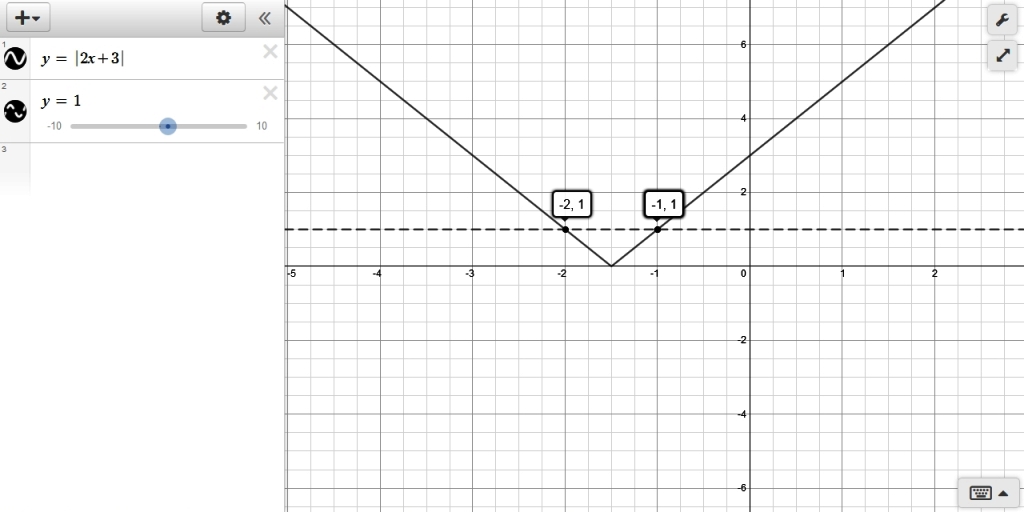
you can confirm the solution is good by going back to the original equation and replacing x with selected values to see when the equation is true and when the equation is false.
the original equation is 7 - abs(2x+3) <= 6
when x is -3, you get 7 - abs(-6+3) = 7 - abs(-3) = 7 - 3 = 4 which is smaller than or equal to 6 so all is good because x is smaller than or equal to -2.
when x is -2, you get 7 - abs(-4+3) = 7 - abs(-1) = 7 - 1 = 6 which is smaller than or equal to 6 so all is still good because x is smaller than or equal to -2.
when x ix 0, you get 7 - abs(0+3) = 7 - abs(3) = 7 - 3 = 4 which is smaller than or equal to 6 so all is still good because x is greater than or equal to -1.
when x is -1, you get 7 - abs(-2+3) = 7 - abs(1) = 7 - 1 = 6 which is smaller than or equal to 6 so all is still good because x is greater than or equal to -1.
when x is -1.5, you get 7 - abs(-3+3) = 7 - abs(0) = 7 - 0 = 7 which is greater than 6 so all is still good because x is not greater than or equal to -1 and x is not smaller than or equal to -2 and you should not get a result smaller than or equal to 6 which you don't.
everything looks good, so your solution is:
x <= -2 or x >- -1
interval notation is as shown above and below:
(-infinity,-2] or [-1,infinity)
|
|
|
| |