Question 901689: 16sin^2(theta)-12=0
what are the solutions on the interval: 0 is less than or equal to theta is less than 2pi
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 16 * sin^2(theta) - 12 = 0
add 12 to both sides to get:
16 * sin^2(theta) = 12
divide both sides by 16 to get:
sin^2(theta) = 12/16 = 3/4
take the square root of both sides to get:
sin(theta) = plus or minus sqrt(3)/2
sin(60) = sqrt(3)/2
60 degrees is therefore your reference angle.
if sin(theta) is positive, x can be in quadrant 1 or quadrant 2.
this makes theta equal to 60 degrees or 120 degrees.
60 degrees in the first quadrant is 60 degrees.
60 degrees in the second quadrant is 180 - 60 = 120 degrees.
if sin(theta) is negative, then x will be in quadrant 3 or quadrant 4.
this makes theta equal to 240 degrees or 300 degrees.
60 degrees in the third quadrant is equal to 180 + 60 = 240 degrees.
60 degrees in the fourth quadrant is equal to 360 - 60 = 300 degrees.
since 2pi is equivalent to 360 degrees, your solution in the interval from 0 to 2pi is the same as your solution in the interval from 0 to 360 degrees.
the solutions in the interval from 0 to 360 degrees is:
x = 60, 120, 240, or 300 degrees.
since radians is equal to degrees * pi / 180, your equivalent solution in the interval from 0 to 2pi radians is:
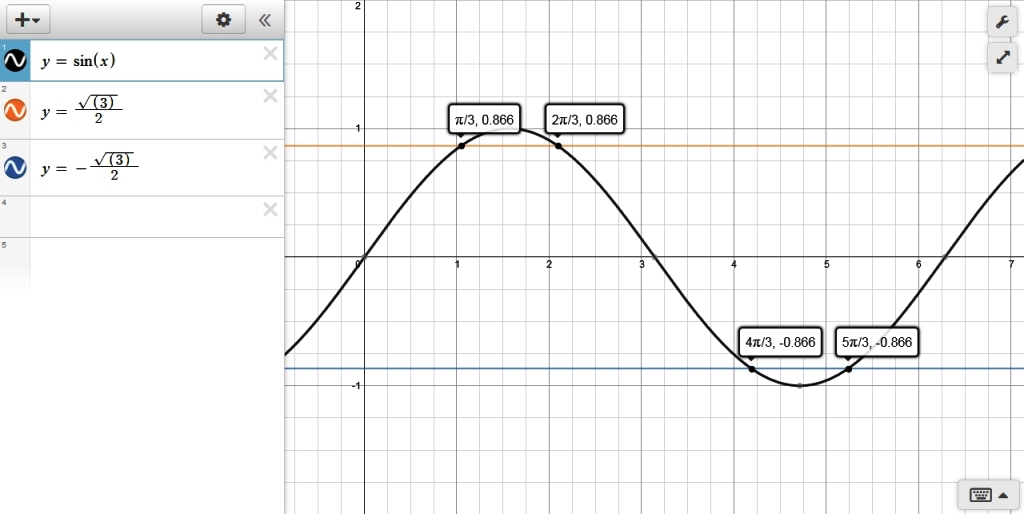
x = pi/3, 2pi/3, 4pi/3, 5pi/3 radians.
a graph of y = sin(x) intersecting with the graph of y = plus or minus sqrt(3)/2 is shown below:
this graph is shown in radians.
|
|
|