Question 901076: Hi,
I am stuck on this problem and need help I am not sure how to do this problem.
using the distance formula,d=sqrt(x2-x1)^2+(y2-y1)^2
what is the distance between point (-2,2) and point (2,-3) rounded to the nearest tenth?
a.4.5 units-i picked
b.57.0 units
c.1.0 units
d.6.4 units
i got this answer i did 2=2=4 and 3+2=5 not sure if its correct.
Found 2 solutions by rothauserc, richwmiller:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! distance(d) = square root of ((X2-X1)^2 + (y2-y1)^2)
we are given two points (-2,2) and (2,-3)
d = square root( (2-(-2))^2 + (-3-2)^2)
d = square root( 16 + 25 ) = square root(41) = 6.4 units
answer d is correct answer
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! Not even close as you know!
What happened to using d=sqrt(x2-x1)^2+(y2-y1)^2
(-2,2) and point (2,-3)
(-2,2)(2,-3)
d=sqrt((x2-x1)^2)+(y2-y1)^2)
d=sqrt(+(2--2)^2)+(-3-2)^2
d=sqrt(+(4)^2)+(-5)^2
d=sqrt(16+25)
d=sqrt(41)
6.40312424
| Solved by pluggable solver: Distance Formula |
The first point is (x1,y1). The second point is (x2,y2)
Since the first point is (-2, 2), we can say (x1, y1) = (-2, 2)
So  , , 
Since the second point is (2, -3), we can also say (x2, y2) = (2, -3)
So  , , 
Put this all together to get:  , ,  , ,  , and , and 
--------------------------------------------------------------------------------------------
Now use the distance formula to find the distance between the two points (-2, 2) and (2, -3)

 Plug in Plug in  , ,  , ,  , and , and 





==========================================================
Answer:
The distance between the two points (-2, 2) and (2, -3) is exactly  units units
The approximate distance between the two points is about 6.40312423743285 units
So again,
Exact Distance:  units units
Approximate Distance: 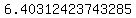 units units
|
|
|
|