Every term of 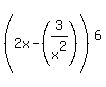 is of the form
is of the form
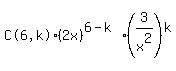 , where k = 0,1,2,3,4,5,6
Write
, where k = 0,1,2,3,4,5,6
Write  as
as 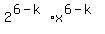 Write
Write  as
as 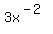
 Write
Write  as
as 
 Rearrange the factors:
Rearrange the factors:
 Add the exponents of x
Add the exponents of x
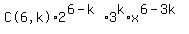 For the term to be independent of x, the power of x
must be 0, since x0 = 1 which contains no x.
So we set the exponent of x equal to 0:
For the term to be independent of x, the power of x
must be 0, since x0 = 1 which contains no x.
So we set the exponent of x equal to 0:

 So we substitute k=2
So we substitute k=2
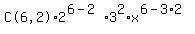

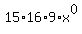

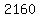 Edwin
Edwin