Question 899892: Decide whether the relation is a function.
{(1, -9), (3, 7), (4, -2), (8, -2), (11, 4)}
Found 3 solutions by ewatrrr, richwmiller, MathLover1:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
{(1, -9), (3, 7), (4, -2), (8, -2), (11, 4)}
Ordered pairs(x,y)(4, -2), (8, -2), , 4 and 8 have same y-values.
relation a function? NO
Answer by richwmiller(17219)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! A function is a special type of relation.
If for  value that is the value that is the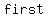 in an ordered in an ordered
pair, there is  one value that is the ( one value that is the ( ) ) 
value ( ) in any of the ordered pairs, then the ) in any of the ordered pairs, then the
relation is a FUNCTION. Or, a function is only if for every  there is only ONE there is only ONE  . But if . But if  different different  values have the same values have the same  value, it's still a value, it's still a  . .
you have {( , ,  ), ( ), ( , ,  ), ( ), ( , ,  ), ( ), ( , ,  ), ( ), ( , ,  )} )}
since in pairs ( , ,  ) and ( ) and ( , ,  ), values ), values  and and  have same value have same value  , it , it 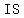 a FUNCTION because if a FUNCTION because if  different different  values have the same values have the same  value, it's still a value, it's still a 
|
|
|