 We want to find the point A on the green line x = -3, such that the red
line that goes from B(3,5) down to it is perpendicular to the black
line 2x+5y=12.
Since point A is on the green line x=-3, its x-coordinate is -3.
Let it's y-coordinate be k. So the point is A(-3,k)
We find the slope of the black line by getting it into slope-intercept
form:
We want to find the point A on the green line x = -3, such that the red
line that goes from B(3,5) down to it is perpendicular to the black
line 2x+5y=12.
Since point A is on the green line x=-3, its x-coordinate is -3.
Let it's y-coordinate be k. So the point is A(-3,k)
We find the slope of the black line by getting it into slope-intercept
form:


 Compare that to
Compare that to
 , we see that the slope of the black line is
, we see that the slope of the black line is 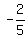 Therefore the slope of the red line is the reciprocal of
Therefore the slope of the red line is the reciprocal of 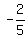 but
with the opposite sign. So the slope of the red line is
but
with the opposite sign. So the slope of the red line is 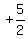 .
Since point A is on the green line x=-3, its x-coordinate is -3.
Let its y-coordinate be k.
We use the slope-formula:
m =
.
Since point A is on the green line x=-3, its x-coordinate is -3.
Let its y-coordinate be k.
We use the slope-formula:
m =  where (x1,y1) = B(3,5)
and where (x2,y2) = A(-3,k)
m =
where (x1,y1) = B(3,5)
and where (x2,y2) = A(-3,k)
m = 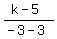


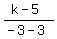


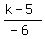 Cross multiply:
Cross multiply:
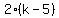

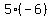



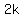




 So the point is A(-3,-10)
Edwin
So the point is A(-3,-10)
Edwin