|
Question 896575: What are the coordinates of points Q and R where Q is on  and R is on and R is on  and a line is drawn from P to intersect with the lines so that P is the midpoint of QR and P(1,1) and a line is drawn from P to intersect with the lines so that P is the midpoint of QR and P(1,1)
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We let the x-component of Q be a, Then since Q is on the line
 , the y-component of Q is found by substituting
a for x in , the y-component of Q is found by substituting
a for x in  and get and get  . So
Q is the point Q(a, . So
Q is the point Q(a,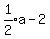 ),
We let the x-component of R be b, Then since R is on the line ),
We let the x-component of R be b, Then since R is on the line
 , the y-component of R is found by substituting
b for x in , the y-component of R is found by substituting
b for x in  and get and get  . So
R is the point R(b,-b+5) . So
R is the point R(b,-b+5)
 We are told that P(1,1) is the midpoint of QR. We use the
midpoint formula:
Midpoint =
We are told that P(1,1) is the midpoint of QR. We use the
midpoint formula:
Midpoint =  Midpoint =
Midpoint =  So we equate those coordinates to the coordinates of P(1,1).
Equating the x-coordinates of P
So we equate those coordinates to the coordinates of P(1,1).
Equating the x-coordinates of P

 Equating the y-coordinates of P
Equating the y-coordinates of P



 Multiply through by 2:
Multiply through by 2:

 So we solve the system by substitution or elimination:
So we solve the system by substitution or elimination:
 Solve the first for a=2-b
Substitute in the second equation:
(2-b)-2b=-2
2-b-2b=-2
2-3b=-2
-3b=-4
b=
Solve the first for a=2-b
Substitute in the second equation:
(2-b)-2b=-2
2-b-2b=-2
2-3b=-2
-3b=-4
b= a=2-b
a=2-
a=2-b
a=2- a=
a=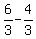 a=
a= So the point
So the point 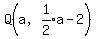 becomes: becomes:
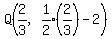
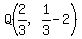
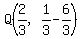
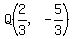 So the point R(b,-b+5) becomes:
So the point R(b,-b+5) becomes:
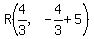
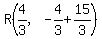
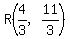 Edwin
Edwin
|
|
|
| |