|
Question 896344: Please find the domain of the following function:
sqrt(2x^3-x^2-18x+9)
Found 2 solutions by Theo, stanbon:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you want to find out the intervals where the square root is positive.
those intervals will be your domain.
start with 2x^3 - x^2 - 18x + 9 = 0
fortunately this factors cleanly.
if not, then you probably would need to graph the equation to see where the intervals lie.
graphing is the easiest way if you have a graphing calculator handy.
i did both.
first the factoring method.
your equation to factor is:
2x^3 - x^2 - 18x + 9 = 0
break this up into 2 separate parts as shown below:
(2x^3 - x^2) - (18x - 9) = 0
factor the first part to get:
x^2 * (2x - 1) - (18x - 9) = 0
factor the second part so the expression in the parentheses will be equal to 2x - 1.
you get:
x^2 * (2x - 1) - 9 * (2x - 1) = 0
factor out the common term of (2x - 1) to get:
(x^2 - 9) * (2x - 1) = 0
x^2 - 9 can further be factored into (x - 3) * (x + 3)
your equation becomes:
(x - 3) * (x + 3) * (2x - 1) = 0
the roots of this equation are:
x = 3
x = -3
x = 1/2
those are the values of x where the value of the equation is equal to 0.
in other words, the graph of the equations crosses the x-axis at those values of x.
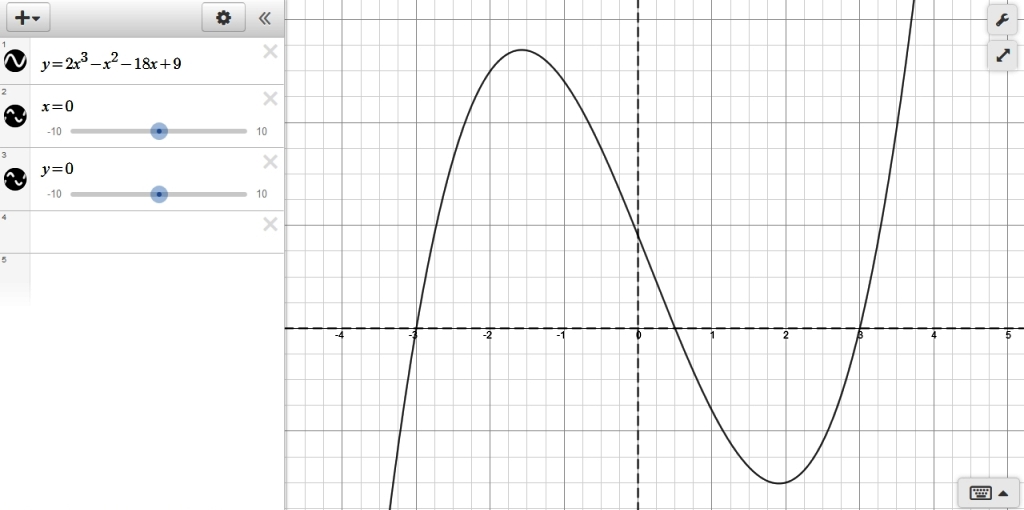
you now need to test each interval to see whether the graph is negative or positive in those intervals.
first interval is x < -3
graph is negative there.
second interval is x > -3 and < 1/2
graph is positive there.
third interval is x > 1/2 and < 3
graph is negative there.
fourth interval is x > 3
graph is positive there.
your domain is the intervals where the square root of the equation is not negative.
those intervals will be:
-3 <= x <= 1/2
x >= 3
here's a graph of the equation within the square root sign where you wanted to find the intervals where it was positive and where it was negative.
the equation used is y = 2x^3 - x^2 - 18x + 9
here's a graph of the equation you wanted to find the domain for.
that equation is y = sqrt(2x^3 - x^2 - 18x + 9)
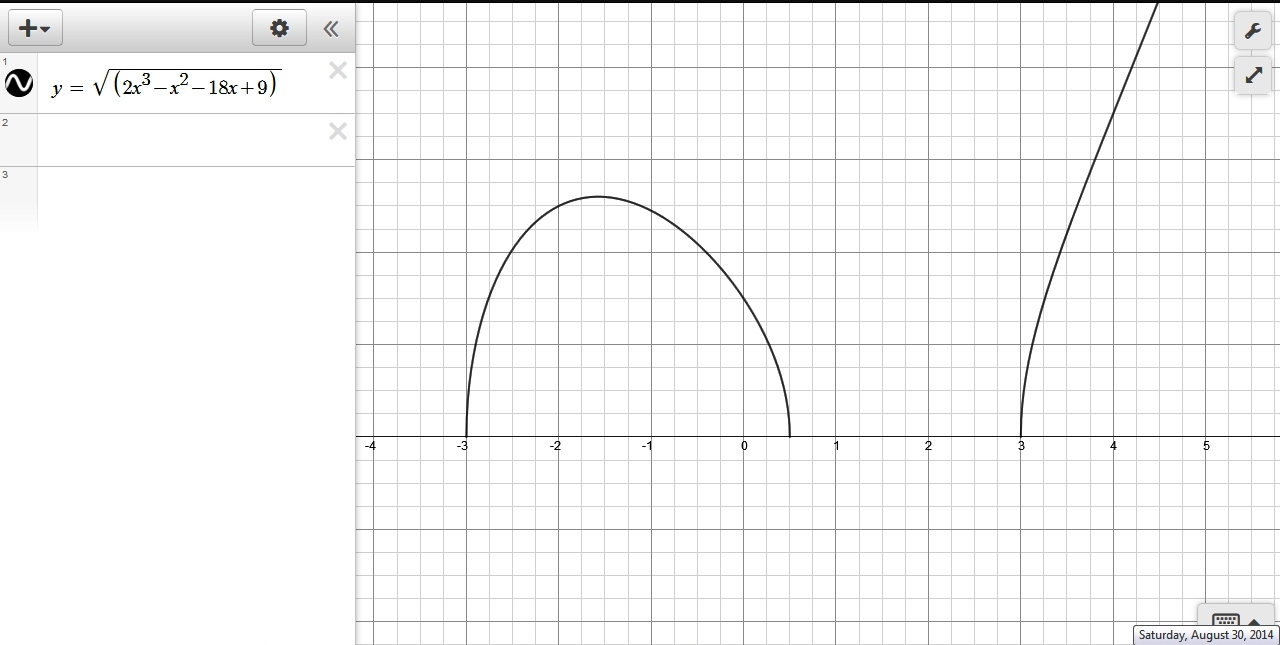
since the intervals where the square root is negative are invalid because they don't result in any real values, the graph is missing in those intervals.
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the domain of the following function:
sqrt(2x^3-x^2-18x+9)
----
Solve:: 2x^3 - x^2 - 18x + 9 >= 0
Factor::
x^2(2x-1) -9(2x-1) >= 0
-----
(2x-1)(x^2-9) >= 0
------
Equality solutions:
x = -3, x = 1/2, x = 3
------
Inequality solutions::
Tests::
If x = -10 you get, -*+ > 0 which is false
If x = -1 you get, -*- > 0 which is true
If x = 2 you get, +*- > 0 whixh is false
If x = 10 you get, +*{ > 0 which is true
------
Solution:: Domain = [-3,1/2] U [3,+oo)
================================
Cheers,
Stan H.
=======================
|
|
|
| |