Question 895479: Problem regarding 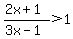
I actually know how to solve it. I solved in many ways because I wanted to be an expert of it.
I plotted a graph taking  and highlighted the area. I got the answer 1/3 < x < 2 and highlighted the area. I got the answer 1/3 < x < 2
I solved it in this way too..
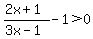 and got the same solution. and got the same solution.
But my problem is... WHY CAN'T I CROSS MULTIPLY LIKE THIS???
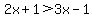
Please don't tell "Because we don't know whether 'x' is plus or minus which changes > to < I want a better explanation. Thank you so much.
Found 2 solutions by Fombitz, MathTherapy:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Problem regarding 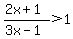
I actually know how to solve it. I solved in many ways because I wanted to be an expert of it.
I plotted a graph taking  and highlighted the area. I got the answer 1/3 < x < 2 and highlighted the area. I got the answer 1/3 < x < 2
I solved it in this way too..
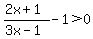 and got the same solution. and got the same solution.
But my problem is... WHY CAN'T I CROSS MULTIPLY LIKE THIS???

Please don't tell "Because we don't know whether 'x' is plus or minus which changes > to < I want a better explanation. Thank you so much.
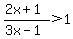 , with , with 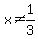 , since this value would render the inequality UNDEFINED , since this value would render the inequality UNDEFINED
In this case, you certainly CAN cross-multiply 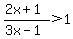 to get: to get: 
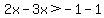

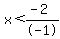 ------ Note that the INEQUALITY sign changed, since DIVISION by a negative value (- 1) dictates such ------ Note that the INEQUALITY sign changed, since DIVISION by a negative value (- 1) dictates such
Therefore, 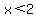
We now have 2 CRITICAL POINTS:  , and , and 
The intervals to test for values to make the inequality TRUE would then be:
1) 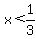 , and , and
2) 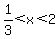
For 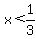 , we can use 0 for x , we can use 0 for x
Does the INEQUALITY PROVE TRUE when this occurs? Let's see!!
With x = 0, 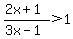 becomes: becomes: 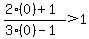
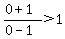 ____ ____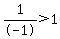 ____ ____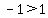 (FALSE) (FALSE)
For 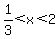 , we can use 1 for x , we can use 1 for x
Does the INEQUALITY PROVE TRUE when this occurs? Let's see!!
With x = 1, 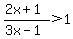 becomes: becomes: 
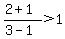 ____ ____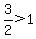 (TRUE) (TRUE)
As seen from the 2 tested intervals, the only solution is: 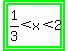
***Another test interval is: 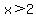 , but I knew that this interval would render the INEQUALITY, false. , but I knew that this interval would render the INEQUALITY, false.
So, your answer is CORRECT!! Good job!!
You can do the check!!
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams,GENERAL
MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,
Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,
GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.
|
|
|