Question 895438: I am stuck on this problem. 2 ln(x)= ln(x-3)+ln(x+1)
I tried doing 2 ln(x)= ln(x^2-2x+3)
then I tried dividing the x to move the xs to the right
2 ln=ln(x-2+3).
Please help!
Found 2 solutions by josgarithmetic, Theo:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! interesting problem because you can get a solution but not if you have to go back to the original equation to confirm that it is true.
in other words, the solution is valid for an intermediate equation but not for the original equation.
your original equation is 2*ln(x) = ln(x-3) + ln(x+1)
since 2*ln(x) is equivalent to ln(x^2), your equation becomes:
ln(x^2) = ln(x-3) + ln(x+1)
since ln(x-3) + ln(x+1) is the same as ln((x-3)*(x+1)), your equation becomes:
ln(x^2) = ln(x^2-2x-3)
this is true if and only if x^2 = x^2-2x-3
x^2 = x^2-2x-3 when x = -3/2.
here's where the conflict comes into play.
if you replace x with -3/2 in the equation of ln(x^2) = ln(x^2-2x-3), you will get .8109... = .8109... which conforms that the value of x = -3/2 is a good solution.
unfortunately, you have to go back to the original equation to confirm that the solution is good.
if you replace x with -3/2 in the equation of 2*ln(x) = ln(x-3) + ln(x+1), you will get an error indication telling you that the solution is not real.
if you graph the equation of ln(x^2) and you graph the equation of ln(x^2-2x-3), you will find that those graphs will intersect at x = -3/2.
that graph is shown below:
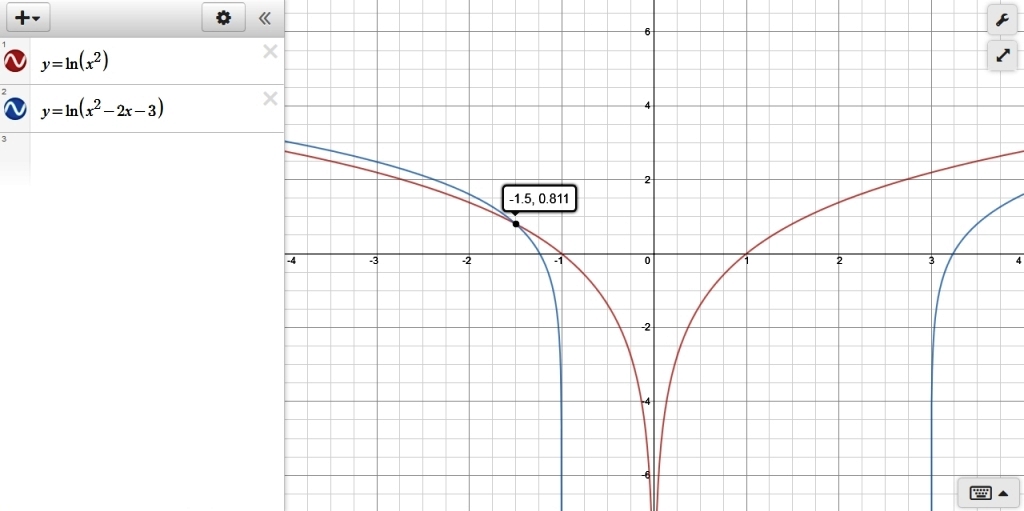
if ou graph the equation of 2*ln(x) and you graph the equation of ln(x-3) + ln(x+1), you will find that those graphs will not intersect because the value of x = -3/2 is not part of the domain since you can't take the log of a negative number.
that graph is shown below:
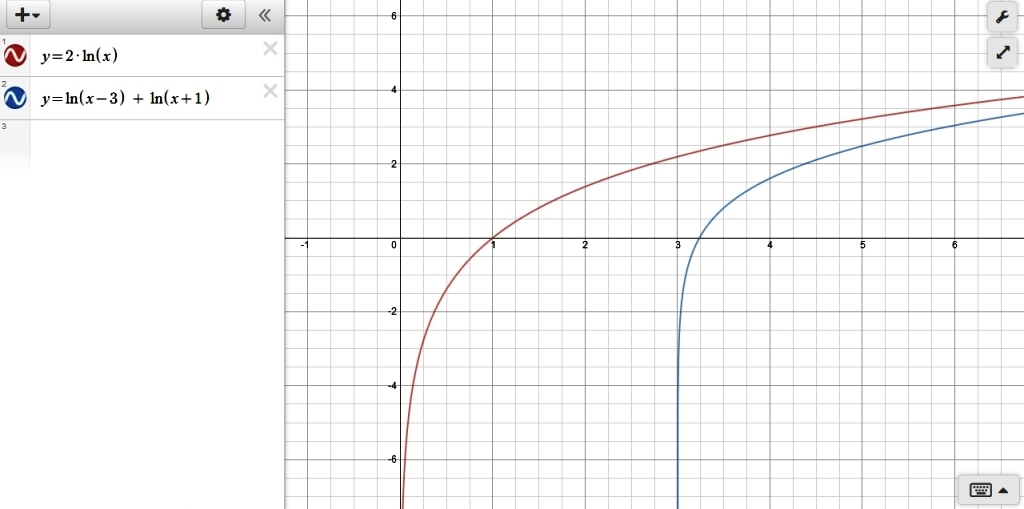
note that, for values of x > 0, the graph of y = 2*ln(x) is identical to the graph of y = ln(x^2)
not also that, for value of x > 0, the graph of y = ln(x-3) + ln(x+1) is identical to the graph of y = ln(x^2-2x-3).
these graphs are identical, but only where the valid domain for each coincides.
their domains are both valid when x > 0.
for example, taking a random value of x > 3, we get:
when x = 5:
y = 2*ln(x) = 3.218875...
y = ln(x^2) = 3.218875...
y = ln(x-3) + ln(x+1) = 2.484906...
y = ln(x^2-2x-3) = 2.484906...
this has also been confirmed graphically for all values of x > 3.
the equatons of y = 2*ln(x) and y = ln(x^2) are identical for all values of x > 0.
when x is less than or equal to 0, the equation of 2*ln(x) is invalid.
the equations of y = ln(x-3) + ln(x+1) and y = ln(x^2 -2x - 3) are identical for all values of x > 3
when x is less than or equal to 3, the equation of ln(x-3) + ln(x+1) is invalid because x-3 is less than or equal to 0.
ln(x+1) is valid for all values of x > -1, but that doesn't count because both halves of that equation have to be valid and ln(x-3) is invalid for any values of x less than or equal to 3.
|
|
|