Question 894458: a father was 30 years old when his daughter was born and the product of their present ages is 736. how old are they now
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Today, y years later:
Father is 30+y;
Daughter is 0+y;
Do you want to try factoring?
2, 4, 8, 16, 46, 92, 184, 368
A pair there looks like a good possibility.
The meaningful solution is  , the daughter's age.
Father is  .
--
STUDENT STILL CONFUSED
Daughter was born y years ago. We do not yet know y. The father was 30 years old at that time.
Let fathers age TODAY be  ;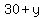
Daughter's age TODAY is  ;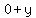
She was born y years ago, and her age at birth was 0.
TODAY at present, the product of their ages is  .
We want to solve this equation for y. This equation is the same as  ;
simplify:
 ---Quadratic Equation in standard form.
We should factor the quadratic expression if it is possible.
Here is a list of factorizations of 736, ignoring signs:
-
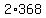
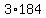
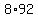
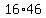
Which of those pair of factors will be able, with appropriate choice of signs, give
a sum of 30 ?
We are trying to find some a and b so that  .
TEST EACH PAIR of  ; ONE of them WILL WORK.
-
When you find which a and b will work, you need to choose the needed signs for a and b.
Remember, the objective right now is to factoirze  .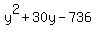
The factorization which works is  .
Next, the objective is to solve this factorized equation.
The Zero-Product rule tells us that either  or  .
One of the solutions is meaningful and the other solution is not.
-
makes sense.
 does not make sense.
NOW we have solved for y.
What is father's age and daughter's age presently, today?
Father:  .
Daughter: .
|
|
|
