Question 894437: A motorboat travels 220km in 4 hours going upstream. It travels
284km going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of the current?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39615)   (Show Source): (Show Source):
You can put this solution on YOUR website! r = rate of boat if c=0
t = time going upstream, 4 hour
u = distance upstream, 220 km
b = distance going back downstream, 284 km
c = rate of the current
________________rate__________time________distance
upstream________r-c____________t__________u
downstream______r+c____________t__________b
The unknown variables are r and c.
RT=D if the uniform rates travel formula for rate, time, distance.

and

 , and , and  , the system; perfectly ready for Elimination Method for each variable. , the system; perfectly ready for Elimination Method for each variable.



-


 , and you know that , and you know that  is a negative number, but you will divide both sides by is a negative number, but you will divide both sides by  ; ;


Look above at the variable assignments, and substitute what was given to compute c and r. You can use the same formulas here in case you find another example travel problem that is in the same general form as this one.
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A motorboat travels 220km in 4 hours going upstream. It travels
284km going downstream in the same amount of time. What is the rate of the boat in still water and what is the rate of the current?
Speed at which it travels, going upstream = 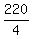 , or 55 km/h , or 55 km/h
Speed at which it travels, going downstream = 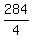 , or 71 km/h , or 71 km/h
Let rate of boat in still water be S, and the current, C
Traveling upstream, it'd be going AGAINST the current, so we can say that: S - C = 55 ------ eq (i)
Traveling downstream, it'd be going WITH the current, so we can say that: S + C = 71 ------ eq (ii)
2S = 126 ------ Adding eqs (i) & (ii)
S, or speed of boat in still water = 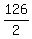 , or , or  km/h km/h
63 - C = 55 ------- Substituting 63 for S in eq (i)
- C = 55 - 63
- C = - 8
C, or speed of current = 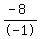 , or , or  km/h km/h
|
|
|