What is the domain and range of the following
rational expression?
f(x)=x+3
_____
x^2-5x-66
f(x) = 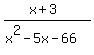 Factor the denominator:
f(x) =
Factor the denominator:
f(x) = 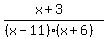 The domain contains all numbers which
can be substituted for x, and an answer
is defined. Denominators cannot be 0
so x cannot be any number that will
cause the denominator to be 0.
DENOMINATOR = (x-11)(x+2)
So x cannot equal to 11 or -2
So the domain is
The domain contains all numbers which
can be substituted for x, and an answer
is defined. Denominators cannot be 0
so x cannot be any number that will
cause the denominator to be 0.
DENOMINATOR = (x-11)(x+2)
So x cannot equal to 11 or -2
So the domain is
 or in interval notation (-
or in interval notation (- ,-2)U(-2,11)U(11,
,-2)U(-2,11)U(11, )
Now we have to find the range.
To do that we first replace f(x) by y and solve for x:
f(x) =
)
Now we have to find the range.
To do that we first replace f(x) by y and solve for x:
f(x) = 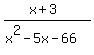 y =
y = 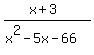 Multiply both sides by the LCD =
Multiply both sides by the LCD = 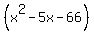
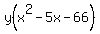 =
= 
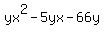 =
=  Get 0 on the right:
Get 0 on the right:
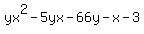 =
=  Get the x terms together:
Get the x terms together:
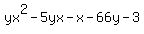 =
=  Factor x out of the second and third terms
Factor x out of the second and third terms
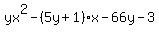 =
=  factor -3 out of the last two terms on the left:
factor -3 out of the last two terms on the left:
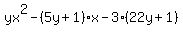 =
=  This is a quadratic equation in x with
a = y, b = -(5y+1), c = -3(22y+1)
We could solve for x, but we only
need the discriminant b²-4ac to be
non-negative, so
b²-4ac = [-(5y+1)]² - 4(y)[-3(22y+1)] =
25y² + 10y + 1 + 12y(22y+1) =
25y² + 10y + 1 + 264y² + 12y =
289y² + 22y + 1 > = 0
The left side has discriminant 22²-4(289)(1) = -672
thus it has no real zeros and represents a parabola which
is always positive.
Therefore the range is "all real numbers" or (-
This is a quadratic equation in x with
a = y, b = -(5y+1), c = -3(22y+1)
We could solve for x, but we only
need the discriminant b²-4ac to be
non-negative, so
b²-4ac = [-(5y+1)]² - 4(y)[-3(22y+1)] =
25y² + 10y + 1 + 12y(22y+1) =
25y² + 10y + 1 + 264y² + 12y =
289y² + 22y + 1 > = 0
The left side has discriminant 22²-4(289)(1) = -672
thus it has no real zeros and represents a parabola which
is always positive.
Therefore the range is "all real numbers" or (- ,
, )
Edwin
)
Edwin