Question 893022: Determine where the function is increasing and where it is decreasing. f(x) = -x^2-8x
I do not understand increasing and decreasing. any info is helpful.
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
You can put this solution on YOUR website! Increasing or decreasing, not complicated concept. Increasing means, becoming greater. Decreasing means, becoming lesser.
As simple as that. Your function is a parabola, so seeing the coefficient on the leading term is negative,
you know the parabola has a vertex which is a maximum point.
Starting at x from the far left, as you trace to x values toward the right, the function f(x)
has values which become greater as each x value is reached, until the vertex point. This is
the greatest value for the parabola, and as you continue reaching new x values toward the right,
each value for f is less than the f value before it. This means that to the right of the vertex]
of this parabola, f is decreasing.

Where then is this maximum point, vertex?

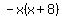
The roots are 0 and -8. The mid value between these roots is -4.
The vertex happens at  . .



-
INCREASING at  ; ;
DECREASING at  . .
|
|
|