use cramers rule to solve the following
Cramer's rule can only be used for independent systems, i.e.,
systems that have only 1 unique solution.
If the system is inconsistent, there will be no solution,
If the system is dependent there will be infinitely many
solution.
We begin by finding the determinant 
. It consists
of just the three columns of x, y, and z coefficients,
in that order, but does not contain the constants, the
three numbers to the right of the equal signs.
.
It has value 
.
Therefore we cannot solve this system by Cramer's rule!
However it may be a dependent system and have infinitely
many solutions.
Now this is probably all your teacher wants you to do at
this point. However, later you will have to find the
general solution for a dependent system, and determine if
it is dependent or inconsistent. So you should
print out the rest of this and save it for future
reference. You may not study this until next year.
But you can easily understand it now.
------------------------------------------
We can find the infinite set of solutions if the
system turns out to be independent, or else determine that it
is inconsistent.
We will create a blank space where the
5x is. Multiply the top equation by -5
Add the top equation to the middle equation
and the -5x cancels the 5x, leaving a blank
space where the 5x was.
Restore the top equation as it was by dividing
it by -5
Next we will create a blank space where the
4x is. Multiply the top equation by -4
Add the top equation to the middle equation
and the -4x cancels the 4x, leaving a blank
space where the 4x was.
Restore the top equation as it was by dividing
it by -4
Now we see that the bottom equation turned out
to be identical to the middle equation.
So we can eliminate the bottom equation entirely
by subtracting it from the middle equation, and
just have:
The fact that this was possible proves that it
is a dependent system, not an inconsistent
system. So there are infinitely many solutions.
So let's find the general solution and some
sample solutions.
So we solve the bottom equation for y:
Substitute in the top equation
Multiply through by 7 to clear the fractions:
So the general solution is
(x,y,z) =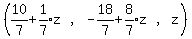 
-------------------------------------------
Som examples of solutions:
If we choose 4 for z, we get
(x,y,z) = 
(x,y,z) = 
(x,y,z) =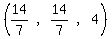 
(x,y,z) = (2,2,4)
So that's a solution.
If we choose 11` for z, we get
(x,y,z) = 
(x,y,z) = 
(x,y,z) = 
(x,y,z) = (3,10,11)
So that's another solution.
If we choose -3 for z, we get
(x,y,z) = 
(x,y,z) = 
(x,y,z) = 
(x,y,z) = (1,-6,-3)
So that's also a solution.
We can get infinitely many solutions because it is
an dependent system. You will find that each
of these three solutions we just found are solutions
to the original system.
There are infinitely many solutions, and we have just
found the general solution and 3 examples of solutions.
Edwin
