SOLUTION: The marks obtained in mathematics by 1000 students is normally distributed with mean 78% and standard deviation 11%. Determine i) What was the highest mark obtained by the lo

Observe the graph below. It has a mean of 0.78, which is on the x-axis
below the highest point on the curve. See the question mark
on the x-axis?  We want to find the number that goes there so
that the area between the x axis and the normal curve will be
25% of 0.25.  The number that goes where the question mark is
will be less than 0.78.

OUR ACTUAL NORMAL CURVE:


Here is how we find the value that goes on the x-axis where the
question mark is.

In order to do that we must find the corresponding point on the
STANDARD normal curve.  Notice that the STANDARD normal curve 
does not have an x-axis, but has a z-axis instead.  Notice that
instead of having 78 below its highest point, it has 0 below its
highest point.  (The z-score of the mean 78 on the actual normal
above corresponds to 0 on the STANDARD normal curve below.

STANDARD NORMAL CURVE


We can either use a normal table or a TI-83 or 84 calculator to find
the value at the question mark on the STANDARD normal curve, so we
can convert it to the question mark on the original normal curve at
the top.

There are two kinds of STANDARD normal tables. The easiest table is the 
kind that has NEGATIVE z-values.  There is one at this site:

http://math2.org/math/stat/distributions/z-dist.htm

We find the closest value to 25% or 0.25 in the body of the table,
which is 0.25143.  We notice that that is the area to the left of 
z = -0.67.

So -0.67 is the value where the question mark is located on the
STANDARD normal curve.

Finally we must convert that z-score of -0.67 on the STANDARD normal
curve to our ACTUAL normal curve at the top by this conversion formula

 

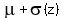where  and , and 

   

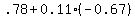
, round to 

So now we know the answer. The question mark on our original curve
has the value  0.706 which means that 25% of that class scored 70.6%
or lower.  That's the same as saying that the highest mark of the
lowest 25%.  [That's also known as the "first quartile" since it is 
the highest value of the lowest 25%.

OUR ACTUAL NORMAL CURVE:


-------------------------------

The middle 90% leaves 10% to split between the right and the
left tail, so that each has 5% of the area.  So we want to
know the values of x on the graph below where the two question
marks are.

OUR ACTUAL NORMAL CURVE:


so we find the corresponding z-values:



We find the closest value to 5% or 0.05 in the body of the table,
which is 0.05050.  We notice that that is the area to the left of 
z = -1.64.

So -1.64 is the value where the left question mark is located on the
STANDARD normal curve.  Now by symmetry on the normal curve, we know
that the right question mark is at +1.64

We must convert those z-scoresa of -1.64 and 1.64 on the STANDARD normal
curve to our ACTUAL normal curve by this conversion formula

 

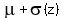First for z=-1.64

where  and , and 

   

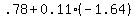
, round to 

And now for for z=+1.64

where  and , and 

   

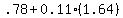
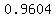, round to 


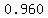The left question mark on our original curve
has the x-value  0.600 and the right question mark has the x-value 0.960

 

Answer: the middle 90% of the students scored between 60.0% and 96.0%.

Edwin