Question 891884: A polynomial P is given.
P(x) = x^6-7x^3-8
(a) Find all zeros of P, real and complex. (Enter your answers as a comma-separated list. If a root has multiplicity greater than one, only enter the root once.)
x=?
b) Factor P Completely
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! Possible maximum of six roots. Try synthetic division on 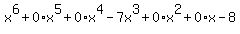 and check the possible roots plus-and-minus 1,2,4,8.
According to that, roots found: -1, 2
Those seem to be the only rational roots, leaving as quotient coefficients 1,1,3,-2,4 for the polynomial factor 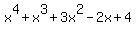 . There are no other real zeros or roots (graphing feature of google was used to see that).
Should be some other complex roots. Maybe a substitution for x^3 as another temporary variable may help. If you will do this, then you can factorize this way:
 .
You can derive for yourself OR look for sum and difference of cubes in a book to obtain;
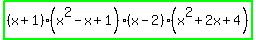 , and from these, you can both see the roots already found, and can find the other four complex roots using the general solution for a quadratic formula.
|
|
|
