SOLUTION: (x^2-18x+65)/(2x-1)(16x^2-26x+9) * (16x^2-28x+10)(8x-9)/(x^3+2x^2)(24x^2-150x+150) What I have tried was distributing each parenthesis with the one right next to it. Then I

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: (x^2-18x+65)/(2x-1)(16x^2-26x+9) * (16x^2-28x+10)(8x-9)/(x^3+2x^2)(24x^2-150x+150) What I have tried was distributing each parenthesis with the one right next to it. Then I      Log On


   

Question 891497: (x^2-18x+65)/(2x-1)(16x^2-26x+9) * (16x^2-28x+10)(8x-9)/(x^3+2x^2)(24x^2-150x+150)


What I have tried was distributing each parenthesis with the one right next to it. Then I was going to multiply across and then divide. When I comepleted these steps i ended up with 360x^6+18624x^2+28884x-35100 / 24x^5-150x^4-4800x^3-20400x^2+2112x-9 ... as you can see this was before I had divided but it just didnt look correct so I was stuck. Thank You for your help!
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I believe you meant
%28x%5E2-18x%2B65%29%2F%28%282x-1%29%2816x%5E2-26x%2B9%29%29 * %28%2816x%5E2-28x%2B10%29%288x-9%29%29%2F%28%28x%5E3%2B2x%5E2%29%2824x%5E2-150x%2B150%29%29 .
That is a pretty complicated expression, and you would not be given that as a problem unless it could be simplified.
Divide and conquer.
You need to do a lot of factoring.
Except for {2x-1) and (8x-9), each polynomial factor in your expression can be written as a product of simpler factors.
x%5E2-18x%2B65=%28x-13%29%28x-5%29
16x%5E2-26x%2B9=%282x-1%29%288x-9%29
16x%5E2-28x%2B10=2%282x-1%29%288x-9%29
x%5E3%2B2x%5E2=x%5E2%28x%2B2%29
24x%5E2-150x%2B150=2%2A3%284x-5%29%28x-5%29
Written as a product of the simplest factors, the complicated expression above is:

There is more than one factor that appears in both the numerator and the denominator. Those factors "cancel out", and that allows you to simplify the expression.
The question is how to "show your work" for that simplification.
Some instructors allow you to cross out such factors, while others do not like the messy look of all those cross-outs.
Many believe that it will lead you to start incorrectly crossing out portions of an expression without understanding the logic behind the procedure.
If crossing out is not allowed, you have to rearrange the factors, so that the matching factors are grouped together as a factor equal to 1, separated from the unmatched factors:
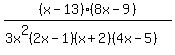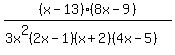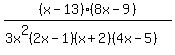
=%28x-13%29%288x-9%29%2F%283x%5E2%282x-1%29%28x%2B2%29%284x-5%29%29*2%282x-1%29%288x-9%29%28x-5%29%2F%282%282x-1%29%288x-9%29%28x-5%29%29=%28x-13%29%288x-9%29%2F%283x%5E2%282x-1%29%28x%2B2%29%284x-5%29%29*1=%28x-13%29%288x-9%29%2F%283x%5E2%282x-1%29%28x%2B2%29%284x-5%29%29

CHECKING:
1) Do the degrees of numerator and denominator make sense?
The degrees of numerator and denominator in the simplified final expression are 2 and 5 (the denominator degrees being 3 units higher).
The degrees of numerator and denominator in the original expression are 5 and 8, with the denominator degree being 3 units higher, which is reassuring.
2) Choosing an easy value for x , we can see if both expressions give us the same value.
In a different case, I would choose x=0 , but in this case, it would make the denominator zero, and would not help me detect a possible mistake in my calculations.
For x=1 , the value of the simplified final expression is
.
For x=1 , the value of the original expression is
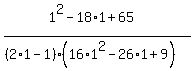%281%5E2-18%2A1%2B65%29%2F%28%282%2A1-1%29%2816%2A1%5E2-26%2A1%2B9%29%29 *
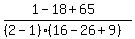=%281-18%2B65%29%2F%28%282-1%29%2816-26%2B9%29%29 * %28%2816-28%2B10%29%288-9%29%29%2F%28%281%2B2%29%2824-150%2B150%29%29
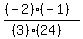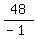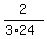=%2848%29%2F%28%281%29%28-1%29%29 * %28%28-2%29%28-1%29%29%2F%28%283%29%2824%29%29 = 48%2F%28-1%29 * 2%2F%283%2A24%29 = -96%2F72=-4%2F3
Though not foolproof, those checks are reassuring (and easy to do).