|
Question 890433: The function f is defined by f(x)=-2x^2-6x+7, x<-2. Find the inverse function and state the corresponding domain and range.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! see the following graph.
see below the graph for further comments.
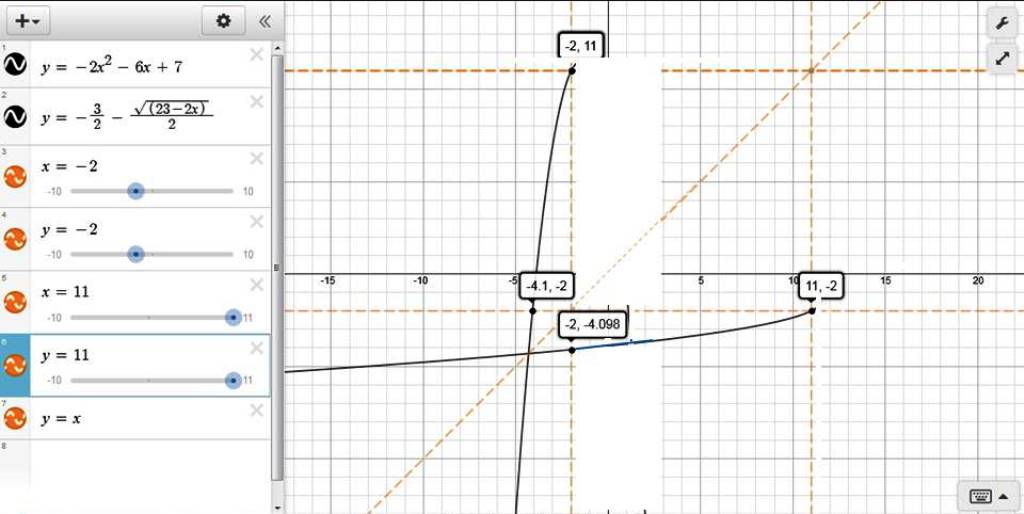
the domain of the original equation is x <= -2
the range of the original equation is y <= 11
the domain of the inverse equation is x <= 11
the range of the inverse equation is y <= -2
that's what happens with inverse equations.
the domain of the original equation becomes the range of the inverse equation.
the range of the original equation becomes the domain of the inverse equation.
the inverse function is found by solving for x and then exchanging x with y.
the inverse function is also found by exchanging x with y and then solving for y.
either way, you get x exchanged with y.
the only difference is when you do it.
with a quadratic equation, you find the inverse equation by using the completing the square method.
i'll show you how by exchanging x with y first and then solving for y.
your original equation is f(x) = -2x^2 - 6x + 7
set y = f(x) and you get:
y = -2x^2 - 6x + 7
exchange y with x and you get:
x = -2y^2 - 6y + 7
here is where you want to complete the square.
re-arrange the terms so that all the y's are on one side of the equation and all the x's and constants are on the other side of the equation.
I added 2y^2 and 6y to both sides of the equation and I subtracted x from both sides of the equation to get:
2y^2 + 6y = 7 - x
now you need to make the coefficient of the x^2 term equal to 1, so divide both sides of the equation by 2 to get:
y^2 + 3y = (7-x)/2
now take 1/2 the coefficient of the y term and complete the square to get:
(y+3/2)^2 = (7-x)/2 + (3/2)^2
simplify to get:
(y+3/2)^2 = (23-2x)/4
i'll show you how the simplification on the right side of the equation was done later.
take the square root of both sides of the equation to get:
(y+3/2) = +/- sqrt((23-2x)/4)
you can simplify the right sides of the equation by taking the 4 out from under the square root sign to get:
(y+3/2) = +/- sqrt(23-2x)/2
subtract 3/2 from both sides of the equation to get:
y = -3/2 +/- sqrt(23-2x)/2
since y needs to be less than or equal to 2, we only need the bottom half of that inverse equation, which is:
y = -3/2 - sqrt(23-2x)/2
the simplification on the right side of the equation that i mentioned above that i would show you later is done as follows:
start with:
(7-x)/2 + (3/2)^2
square (3/2) to get 9/4.
expression becomes:
(7-x)/2 + 9/4
multiply (7-x)/2 by 2/2 to get:
(14-2x)/4 + 9/4
combine the numerators under the common denominator to get:
(14 - 2x + 9) / 4
combine like terms to get:
(23 - 2x) / 4
the simplification is complete.
some editing of the graph had to be done unless I wanted to graph manually.
this was because you have to show graph the whole equation and can't arbitrarily tell the graphing software to only take it up to a certain point, like show the graph from x = - infinity to x = -2 and don't show the rest.
i did the best i could to show you only the pieces of each graph that were applicable.
if the equations are inverses of each other, they will be reflections across the line y = x.
that line was shown along with points that were directly opposite each other.
the point (-2,11) on the original equation becomes (11,-2) on the inverse equation.
the point (-4.1,-2) on the original equation becomes (-2,-4.1) on the inverse equation.
|
|
|
| |