|
Question 89036: Find the slope of the line passing through the points (-1, -2) and (1, 4).
Found 2 solutions by jim_thompson5910, Edwin McCravy:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the slope of the line passing through the points (-1, -2) and (1, 4).
The graphical way:
Plot those two points:
 Draw a line through them:
Draw a line through them:
 Start at the bottom point and draw a horizontal line until you
reach a point directly in line vertically with the other point:
Start at the bottom point and draw a horizontal line until you
reach a point directly in line vertically with the other point:
 This line is 2 units long, as you can see by using the x-axis as
a ruler. It's length called the "change in x", which is also
called the "horizontal change" of just the "RUN". Since to draw
it we had to move our pencil to the RIGHT, we consider it positive,
+2. (If we had to go left we would give
it a negative sign.). So we label the RUN as +2:
This line is 2 units long, as you can see by using the x-axis as
a ruler. It's length called the "change in x", which is also
called the "horizontal change" of just the "RUN". Since to draw
it we had to move our pencil to the RIGHT, we consider it positive,
+2. (If we had to go left we would give
it a negative sign.). So we label the RUN as +2:
 From the end of the "RUN", we draw a vertical line to the
second point.
From the end of the "RUN", we draw a vertical line to the
second point.
 This line is 6 units long, as you can see by using the y-axis as
a ruler. It's length called the "change in y", which is also
called the "vertical change" of just the "RISE". Since to draw
it we had to move our pencil UPWARD, we consider it positive,
+2. (If we had to go DOWNWARD we would give
it a negative sign.). So we label the RISE as +6:
This line is 6 units long, as you can see by using the y-axis as
a ruler. It's length called the "change in y", which is also
called the "vertical change" of just the "RISE". Since to draw
it we had to move our pencil UPWARD, we consider it positive,
+2. (If we had to go DOWNWARD we would give
it a negative sign.). So we label the RISE as +6:
 Now the slope is defined as
Now the slope is defined as 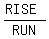 = = 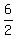 = 3.
That's the slope, m = 3
Edwin = 3.
That's the slope, m = 3
Edwin
|
|
|
| |