Question 890286: Please help!!! I do not feel comfortable with my answers.
In 2010 almost 15 million workers belonged to trade unions, constituting 11.9% of the total labor force. Choose 15 workers at random. What is the probability that exactly one-third of them belong to a trade union? At least one-third? What is the probability that at least 9 did not belong?
1.) P(exactly one-third)= C(15,5)(.881)^5(.119)^10=.0000009?
2.) P(at least one-third)=P(5) =C(15,5)(.881)^5(.119)^10 =.00000091
P(6) =C(15,6)(.881)^6(.119)^9 =.000011
P(7) =C(15,7)(.881)^7(.119)^8 =.000107
P(8) =C(15,8)(.881)^8(.119)^7 =.00079
P(9) =C(15,9)(.881)^9(.119)^6 =.0045
P(10)=C(15,10)(.881)^10(.119)^5=.02
P(11)=C(15,11)(.881)^11(.119)^4=.068
P(12)=C(15,12)(.881)^12(.119)^3=.168
P(13)=C(15,13)(.881)^13(.119)^2=.286
P(14)=C(15,14)(.881)^14(.119)^1=.303
P(15)=C(15,15)(.881)^15(.119)^0=.1495
P(5)+P(6)+P(7)+P(8)+P(9)+P(10)+P(11)+P(12)+P(13)+P(14)+P(15)=.99990891?
3.)P(at least 9 do not belong)
=P(0)=C(15,0)(.881)^0(.119)^15=.000000000000014
P(1)=C(15,1)(.881)^1(.119)^14=.0000000000015
P(2)=C(15,2)(.881)^2(.119)^13=.000000000078
P(3)=C(15,3)(.881)^3(.119)^12=.0000000025
P(4)=C(15,4)(.881)^4(.119)^11=.000000056
P(5)=C(15,5)(.881)^5(.119)^10=.00000091
P(6)=C(15,6)(.881)^6(.119)^9 =.000011
P(7)=C(15,7)(.881)^7(.119)^8 =.000107
P(8)=C(15,8)(.881)^8(.119)^7 =.00079
P(9)=C(15,9)(.881)^9(.119)^6 =.0045
P(0)+P(1)+P(2)+P(3)+P(4)+P(5)+P(6)+P(7)+P(8)+P(9)=.00091?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! formula for binomial probability is:
p(x) = nCx * p^x * q^x
p is the probability of the event occurring.
q is the probability of the event not occurring.
in your problem:
p = .119 = probability that a person does belong to a trade union.
q = .881 = probability that a person does not belong to a trade union.
for p(x = 5), the equation should be C(15,5) * (.119)^5 * (.881)^10 = .020185
looks like you reversed p and q.
for p(x >= 5), it appears you got p and q mixed up and you didn't include p(x) = 5 as well since the problem states at least 5 which means 5 and above.
make those 2 corrections and you should be ok.
for p(at least 9 didn't belong) you had a couple of problems again, except that you didn't mix up p and q, probably because you had them mixed up in the first place.
first problem is that p(at least 9 didn't belong) means you need to get p(9) or greater which would be the sum of p(9) + p(10) + p(11) + p(12) ..... + p(15).
p in this case would be the probability that a person did not belong which would make p = .881 and q = .119.
this is the part that you got right, probably by accident.
the other way you could have solved the third part is as follows:
if 9 or greater didn't belong, then 6 or less did belong, so the probability of 9 or greater didn't belong is equal to the probability that 6 or less did belong.
in that case, the formula would have been:
p(x <= 6) = sum of p(x) from x = 0 to 6, where p = probability that a person did belong = .119 and probability that a person didn't belong = .881.
my calculations in the first picture used this second alternative.
my calculations in the second picture used the first alternative.
nCx can also be shown as C(n,x) as you show it.
here's my first picture.
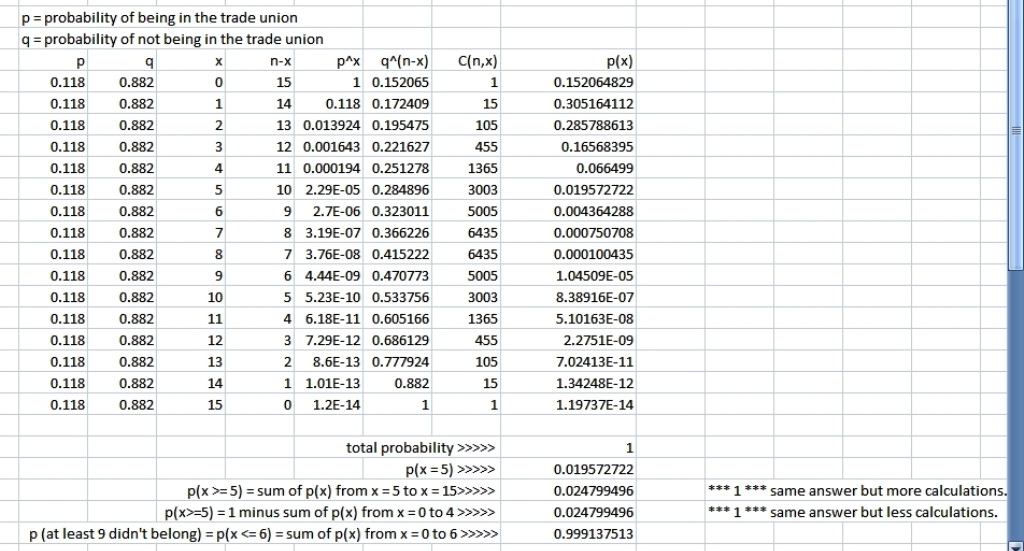
here's my second picture.
you can see that p and q are reversed in this one.
you can also see that p(9 or greater not being in the trade union) from the second picture is the same answer as p(6 or less being in the trade union) from the first picture.
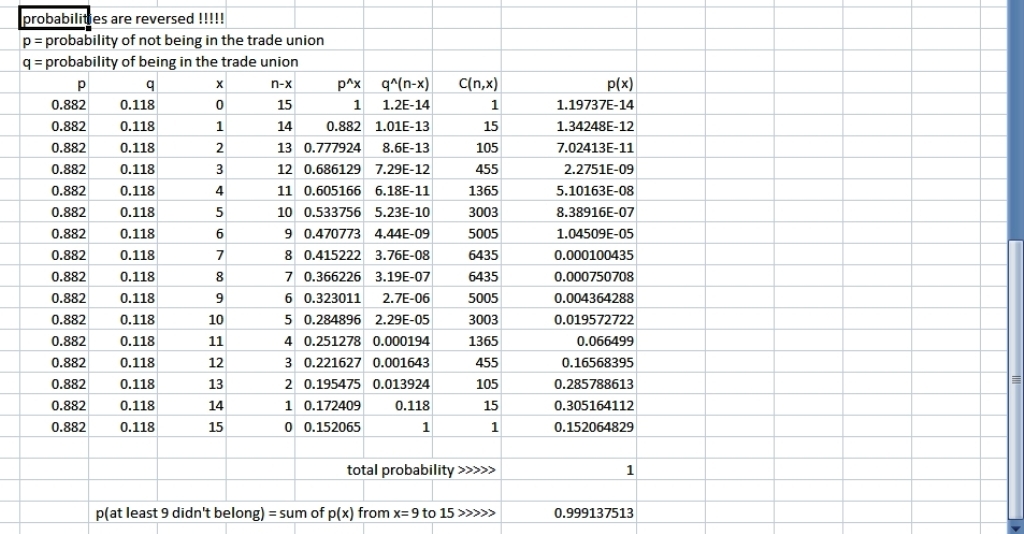
try it out.
see if you get the same answers as me.
if not, let me know and we'll both work on finding out why.
|
|
|