Here are all 36 rolls.
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
Here are all the rolls with a combined value of '9' or over:
(3,6)
(4,5) (4,6)
(5,4) (5,5) (5,6)
(6,3) (6,4) (6,5) (6,6)
There are 10 of them, so the probability of getting a roll
with a combined value of '9' or over is 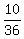 or
or  Here are the rolls of '7' or '8':
(1,6)
(2,5) (2,6)
(3,4) (3,5)
(4,3) (4,4)
(5,2) (5,3)
(6,1) (6,2)
There are 11 of them, so the probability of getting a roll
with a '7' or '8' is
Here are the rolls of '7' or '8':
(1,6)
(2,5) (2,6)
(3,4) (3,5)
(4,3) (4,4)
(5,2) (5,3)
(6,1) (6,2)
There are 11 of them, so the probability of getting a roll
with a '7' or '8' is 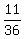 .
Here are the rolls less than a '7':
(1,1) (1,2) (1,3) (1,4) (1,5)
(2,1) (2,2) (2,3) (2,4)
(3,1) (3,2) (3,3)
(4,1) (4,2)
(5,1)
There are 15 of them, so the probability of getting a roll
less than a '7' is
.
Here are the rolls less than a '7':
(1,1) (1,2) (1,3) (1,4) (1,5)
(2,1) (2,2) (2,3) (2,4)
(3,1) (3,2) (3,3)
(4,1) (4,2)
(5,1)
There are 15 of them, so the probability of getting a roll
less than a '7' is  or
or 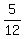 .
Rolls | Probability | Winning | Expectation
------------------------------------------------------------------------
'9' or over | 10/36 | $1.05 | (10/36) × $1.05 = $0.29 1/6
'7' or '8' | 11/36 | -$3.00 | (11/36) × -$3.00 = -$0.91 2/3
less than '7'| 15/36 | $0.60 | (15/36) × $0.60 = $0.25
------------------------------------------------------------------------
Totals | 36/36=1 | | -$0.37 1/2
The expectation is
.
Rolls | Probability | Winning | Expectation
------------------------------------------------------------------------
'9' or over | 10/36 | $1.05 | (10/36) × $1.05 = $0.29 1/6
'7' or '8' | 11/36 | -$3.00 | (11/36) × -$3.00 = -$0.91 2/3
less than '7'| 15/36 | $0.60 | (15/36) × $0.60 = $0.25
------------------------------------------------------------------------
Totals | 36/36=1 | | -$0.37 1/2
The expectation is 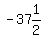 cents. That means if you play
the game many times, you will average losing
cents. That means if you play
the game many times, you will average losing 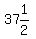 cents per game.
Edwin
cents per game.
Edwin