SOLUTION: Please help me with learning how to factor this polynomial. 8a^3-27

Please help me with learning how to factor this polynomial. 
8a³ - 27

This is the difference of two cubes.

Notice that 
8 is the cube of 2
x³ is the cube of x
27 is the cube of 3

So the cube root of 8a³ is 2a and
the cube root of 27 is 3.

The difference (respectively, sum) of two cubes is 
divisible by the difference (respectively, sum) of
their cube roots.  

There are two methods:

Method 1:
Use long division:

Divide 8a³ - 27 by the difference of the cube roots
2a - 3.

First we have to insert placeholders since 
there is no a² or a terms. So we write 8a³ - 27
as 8a³ + 0a² + 0a - 27

      ________4a²_+__6a +__9
2a - 3)8a³ +  0a² +  0a - 27
       8a³ - 12a²_  
       ¯¯¯¯¯¯12a² +  0a
             12a² - 18a_
             ¯¯¯¯¯¯¯18a - 27
                    18a - 27
                    ¯¯¯¯¯¯¯¯
                           0

So you see it factors as (2a - 3)(4a² + 6a + 9)

==================================================

Method 2:

Memorize the following two rules, the first for the 
SUM of two cubes and the second for the DIFFERENCE of 
two cubes:

 = 

 = 

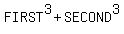where FIRST represents the cube root of the first term, and
SECOND represents the cube root of the second term.

Memorizing these will save you from having to use long division.

In this case, FIRST = cube root of 8a³ which is 2a and
SECOND = cube root of 27, which is 3, so we use the rule for
the DIFFERENCE of two cubes:

 = 

becomes: (2a - 3)(4a² + 6a + 9)

==================================

So if you don't like long division, then memorize the two
rules and use method 2.

Edwin