|
Question 889601: find the equation of the parabola with vertex on the line y=x, the axis of parabola is parallel to the x-axis and passing through (6,-2)and (3,4)
Found 2 solutions by josgarithmetic, lwsshak3:
Answer by josgarithmetic(39625)   (Show Source):
You can put this solution on YOUR website!  , parabola parallel to the horizontal axis.
The line y=x containing the vertex means that the two coordinates of this point are equal in value.
Call this vertex (n,n).
The equation of the parabola can be expressed,  .
The variables, once the given points are substituted, will be a and n. General form should give
a system of equations which we could solve for a and n.
-
Maybe alternatively
 , because this gives a on one side and an expression in terms of n on the other side.
Knowing that a and n are constants, any point on the parabola should give equal expressions for the member on
the right-side.
Using the two given points, those points (6,-2) and (3,4),
and
The two expressions for a must be equal.
 , Divide this by 3;
How is the discriminant?
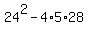
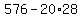
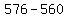
 , a perfect square whole number.
Now, what can be n?
Either  Or 
... Still not finished. We want to use these values for n to get our value for a; probably a single (or maybe not) value. You will have to try each of the solutions for n and find out.
Answer by lwsshak3(11628) (Show Source):
You can put this solution on YOUR website! find the equation of the parabola with vertex on the line y=x, the axis of parabola is parallel to the x-axis and passing through (6,-2)and (3,4)
***
give data shows parabola open rightwards:
Its vertex form of equation: 
(6,-2) 6=(-2-k)^2+h
(3,4) 3=(4-k)^2+h
..
6=4+4k+k^2+h
3=16-8k+k^2+h
subtract
3=-12+12k
12k=15
k=15/12=5/4
..
3=(4-k)^2+h
sub k
3=(4-5/4)^2+h
3=(11/4)^2+h
48/16=121/16+h
h=-121/16+48/16=-73/16
equation:
|
|
|
| |
