Question 889554: Find the value of A when cos 2A=sin 3A.
Found 2 solutions by robertb, Theo:
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! cos2A = sin3A
==> cos2A = cos(90 - 3A)
==> Either 2A = 90 - 3A or 2A = -(90 - 3A)
==> 5A = 90 or 2A = -90 +3A
==> A = 18 or A = 90. These are the solutions from 0 degrees to 360 degrees.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i was able to find the solution graphically.
that solution is shown below in the following 4 pictures.
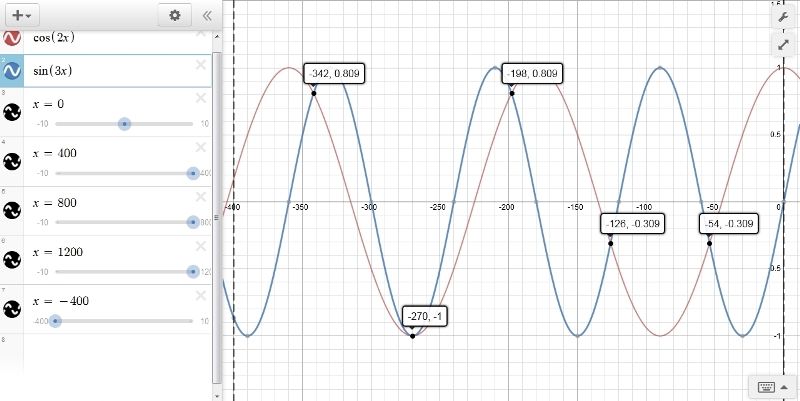
first picture takes you from -400 degrees to 0 degrees.
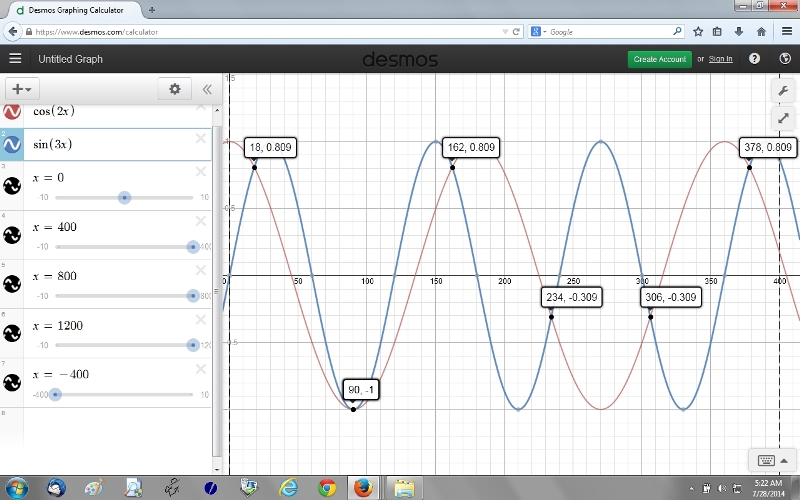
second picture takes you from 0 degrees to 400 degrees.
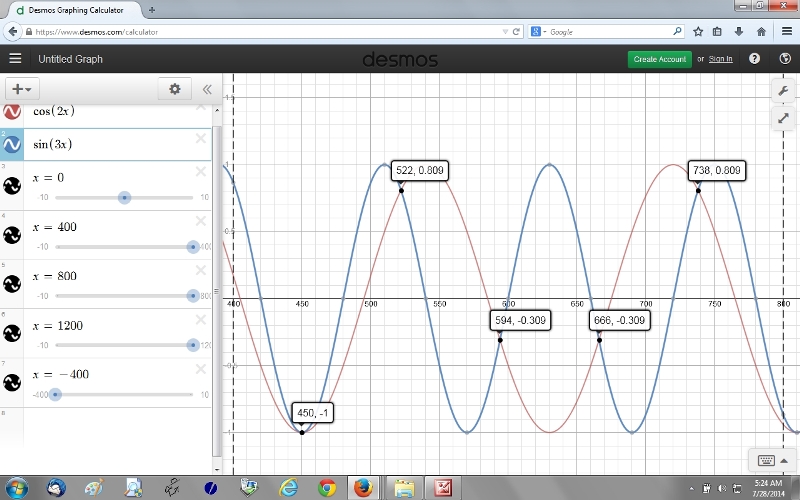
third picture takes you from 400 degrees to 800 degrees.
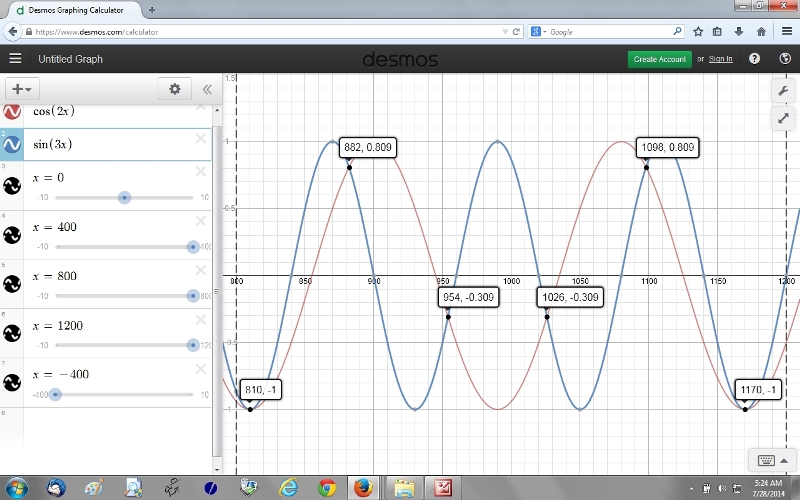
fourth picture takes you from 800 degrees to 1200 degrees.
those graphs are enough to show the periodicity of the solutions.
those solutions and their periodicity are shown here.
x = 18 degrees +/- 360 degrees.
x = 162 degrees +/- 360 degrees.
x = 90 degrees plus or minus 360 degrees.
x = 234 degrees +/- 360 degrees.
x = 306 degrees +/- 360 degrees.
that should be all the possible solutions of the equation cos(2x) = sin(3x).
if you take any one of those solutions and add or subtract 360 from it, you should get the other solutions shown.
for example:
18 - 360 = -342
162 - 360 = -198
90 - 360 = -270
234 - 360 = -126
306 - 360 = -54
look on the first graph and you should see all those solutions.
going the other way, for one period up, you get:
18 + 360 = 378
162 + 360 = 522
90 + 360 = 450
234 + 360 = 594
306 + 360 = 666
look on the second graph and you should see 378.
look on the third graph and you should see the rest of those solutions.
i also found an algebraic solution on the web at the following link:
http://mathcentral.uregina.ca/QQ/database/QQ.09.04/pierre1.html
that solution looked good except for the fact that it appeared to be missing the solution of cos(2x) = sin(3x) = -1
i then decided to use their strategy and solve the equation for myself to see what was missing and why.
my algebraic solution is shown below.
start with cos(2A) = sin(3A)
cos(2A) is equivalent to cos^2(A) - sin^2(A)
sin(3A) is equivalent to sin(A + 2A)
sin(A + 2A) is equivalent to sin(A)*cos(2A) + cos(A)*sin(2A)
sin(2A) is equivalent to 2*sin(A)*cos(A)
sin(A + 2A) is therefore equal to sin(A)*(cos^2(A)-sin^2(A)) + cos(A)*2*sin(A)*cos(A)
replacing the original expressions with their equivalent expressions, we get:
start with cos(2A) = sin(3A) becomes:
cos^2(A) - sin^2(A) = sin(A)*(cos^2(A)-sin^2(A)) + cos(A)*2*sin(A)*cos(A)
we can distribute the multiplication and combine like terms to get:
cos^2(A) - sin^2(A) = sin(A)*cos^2(A) - sin^3(A) + 2*sin(A)*cos^2(A)
we can combine like terms again to get:
cos^2(A) - sin^2(A) = 3*sin(A)*cos^2(A) - sin^3(A)
if we add sin^3(A) to both sides of the equation and we subtract 3*sin(A)*cos^2(A) from both sides of the equation, we get:
cos^2(A) - sin^2(A) - 3*sin(A)*cos^2(A) + sin^3(A) = 0
if we replace cos^2(A) with its identical expression of 1 - sin^2(A), then we get:
1 - sin^2(A) - sin^2(A) - 3*sin(A)*(1-sin^2(A)) + sin^3(A) = 0
if we combine like terms and distribute the multiplication, we get:
1 - 2*sin^2(A) - 3*sin(A) + 3*sin^3(A) + sin^3(A) = 0
if we combine like terms again, we get:
1 - 2*sin^2(A) - 3*sin(A) + 4*sin^3(A) = 0
if we re-arrange the terms in descending order of degrees, we get:
4*sin^3(A) - 2*sin^2(A) - 3*sin(A) + 1 = 0
one of the factors of this equation is sin(A) - 1, which we found through synthetic division.
the equation becomes:
(sin(A)-1) * (4sin^2(A) + 2sin(A) - 1) = 0
one of our solutions will be sin(A) = 1
through the use of the quadratic formula, our other solutions will be:
sin(A) = .3090169944 or sin(A) = .8090169944
solving for A, we get:
A = 18 degrees or A = -54 degrees.
those are our solutions for one period only.
the graph shows us the other solutions from which we could include the periodicity to these solutions.
the solutions that we solved for algebraically are:
18 degrees
-54 degrees
90 degrees
when you use these solutions.....
cos(2*18) = cos(36) = .809.....
sin(3*18) = sin(54) = .809...
cos(2*-54) = cos(-108) = -.309...
sin(3*-54) = sin(-162) = -.309...
cos(2*90) = cos(180) = -1
sin(3*90) = sin(270) = -1
the graphical solution and the algebraic solution now match for all values shown in the algebraic solution so i'm satisfied that the algebraic solution was solved successfully.
|
|
|