SOLUTION: Find the partial fraction decomposition of the rational function. x5 − 3x4 + 3x3 − 4x2 + 8x + 15 divide (x − 2)2(x2 + 2)

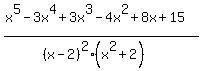
This is analogous to an improper algebra fraction in basic mathematics.  That's
because the numerator is of higher degree than the denominator. 

Since the denominator is of lower degree than the numerator. we have to
multiply the denominator all the way out first and divide the denominator into
the numerator by long division.  This is analogous to what we do in basic
elementary school mathematics when we change an improper fraction to a mixed
number.  

Multiplying the denominator out: 



Then we do the long division, which is analogous to changing an improper
fraction to a mixed number in basic elementary school math:

(The numbers on the right of the x's are to be considered as exponents):

                                x+ 1             
               ---------------------
x4-4x3+6x2-8x+8)x5-3x4+3x3-4x2+8x+15
                x5-4x4+6x3-8x2+8x
                -----------------
                    x4-3x3+4x2+0x+15 
                    x4-4x3+6x2-8x+ 8
                    ----------------
                        x3-2x2+8x+ 7

So this is analogous to changing an improper fraction like  to a mixed 
number 

  

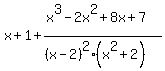The x+1 is analogous to the 3 of  and the fraction is
analogous to the  .

Now we have something analogous to a proper fraction, like the  of :

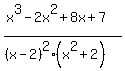 which we now break into partial fractions the usual way:









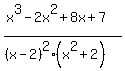
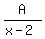
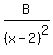
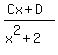
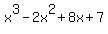
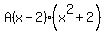
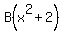
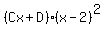
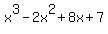
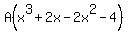
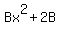
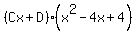
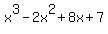
Equating coefficients of x³:

(1)   1 = A + C

Equating coefficients of x²:

(2)  -2 = -2A+B-4C+D

Equating coefficients of x

      8 = 2A+4C-4D

Divide every term by 2:

(3)   4 = A+2C-2D

Equating constant terms:

(4)   7 = -4A+2B+4D

Solve the system of equations consisting of (1),(2),(3), and (4),

getting , , , 



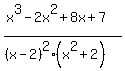
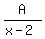
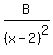
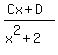becomes:





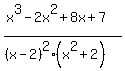
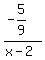
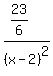
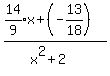
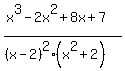
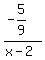
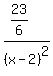
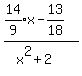 Multiply numerator and denominator of 
first fraction by 9, second fraction by 6, third fraction by 18:

 

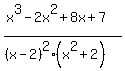
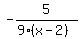
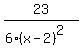
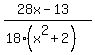Let us not forget about the quotient x+1 in the long division
above.  The partial fraction expansion is:

 

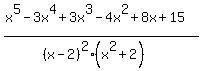
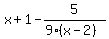
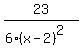
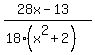Edwin