SOLUTION: Find {{{a}}} such that {{{f(x)=ax^2+5x+6}}} has a minimum value of {{{169/24}}}

Algebra ->  Human-and-algebraic-language -> SOLUTION: Find {{{a}}} such that {{{f(x)=ax^2+5x+6}}} has a minimum value of {{{169/24}}}      Log On


   

Question 889068: Find a such that f%28x%29=ax%5E2%2B5x%2B6 has a minimum value of 169%2F24
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Complete the Square:
f%28x%29=a%28x%5E2%2B%285%2F%28a2%29%29x%2B6%2Fa%29
a%28x%5E2%2B%285%2F%282a%29%29x%2B%285%2F%284a%29%29%5E2-%285%2F%284a%29%29%5E2%2B6%2Fa%29
a%28%28x%2B%285%2F%284a%29%29%29%5E2-%285%2F%284a%29%29%5E2%2B6%2Fa%29
a%28x%2B%285%2F%284a%29%29%29%5E2-a%285%2F%284a%29%29%5E2%2B6, almost finished standard form.

The extreme value happens when x=-%285%2F%284a%29%29 and y=highlight_green%28-a%285%2F%284a%29%29%5E2%2B6=169%2F24%29; there you can solve for a.


-a%2A%2825%2F%2816a%5E2%29%29%2B6=169%2F24
-25%2F%2816a%29%2B6=169%2F24
6-25%2F%2816a%29=169%2F24, LCD is 16*3a.
6%2A16%2A3a-25%2A16%2A3a%2F%2816a%29=169%2A16%2A3a%2F24
6%2A16%2A3a-75=169%2A2%2A3a
169%2A6a-18%2A16a=-75
726a=-75
a=-75%2F726
a=-3%2A25%2F%28242%2A3%29
highlight%28a=-25%2F242%29.

Answer by MathTherapy(10557) About Me  (Show Source):
You can put this solution on YOUR website!
Find a such that f%28x%29=ax%5E2%2B5x%2B6 has a minimum value of 169%2F24


(h, k) is the coordinate point of the vertex of the parabola

h , or x-coordinate of vertex = 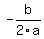-+b%2F2a, or -+5%2F2a



y+=+ax%5E2+%2B+5x+%2B+6, with x+=+-+5%2F2a

k, or y-coordinate of vertex = 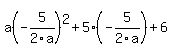a%28-+5%2F2a%29%5E2+%2B+5%28-+5%2F2a%29+%2B+6

k+=+a%2825%2F4a%5E2%29+%2B+-+25%2F2a+%2B+6

k+=+25a%2F4a%5E2+-+25%2F2a+%2B+6    

k+=+25%2F4a+-+25%2F2a+%2B+6

k+=+%2825+-+50+%2B+24a%29%2F4a ------ Multiplying right-side by LCD, 4a

k+=+%28-+25+%2B+24a%29%2F4a   



Since k+=+%28-+25+%2B+24a%29%2F4a, and minimum value = 169%2F24, then: %28-+25+%2B+24a%29%2F4a+=+169%2F24

169(4a)  = 24(- 25 + 24a) ------ Cross-multiplying

676a = - 600 + 576a

676a – 576a = - 600

100a = - 600

a+=+%28-+600%29%2F100, or highlight_green%28highlight_green%28a+=+-+6%29%29

Since a = - 6, then this equation DOES NOT DEPICT a minimum, but a maximum instead, as a < 0.



You can do the check!! 



Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com.

Further help is available, online or in-person, for a fee, obviously. 



For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams,GENERAL

MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra, 

Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,

GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.