Question 889034: 1) A Ferris wheel of a diameter 18.5 m rotates at a constant rate and makes a complete revolution in 10 seconds. If passengers board the lowest car at a height of 3 metres (m) above the ground, determine a Sine function that models the height, ( h ) in metres, of the car relative to the ground as a function of the time, (t) in seconds. Hint: Draw a diagram to help you picture the Ferris wheel and think about what is happening through each of the given transformations!
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website!
the function of the height of a circle from ground level in terms of degrees of angle where 0 degrees is the vertical line from the center of the circle to the ground is:
y = 9.25 - 9.25 * cos(x), where x is the number of degrees.
the graph of that function is shown below:

since the lowest car is 3 feet above the ground, this means that the center of the circle has to also be 3 feet above the ground, so you have to add 3 to this function to account for that.
the function then becomes:
y -9.25 - 9.25 * cos(x) + 3
the graph of that function is shown below:
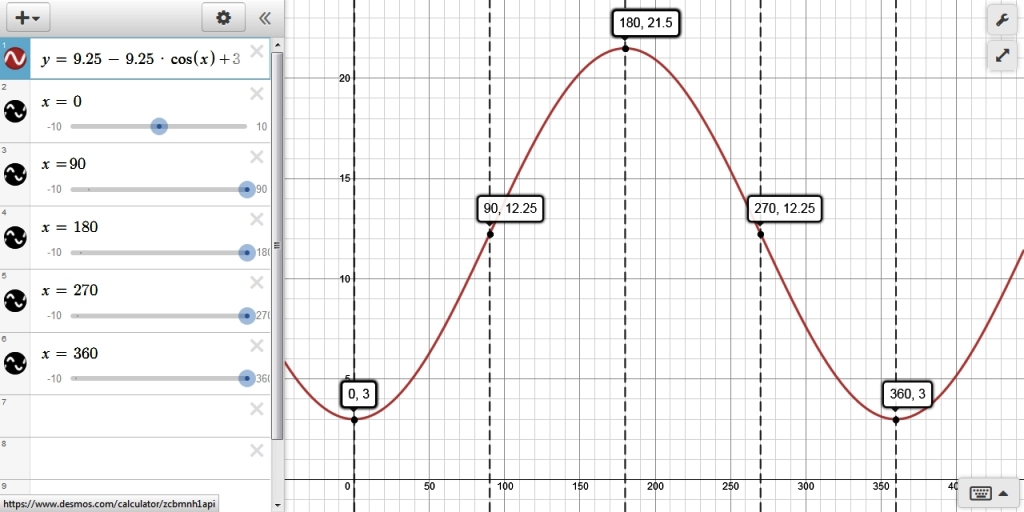
you want to graph the function in terms of time rather than degrees.
the ferris wheel rotates one revolution in 10 seconds.
this means the ferris wheeel rotates 1/10 of a revolution in 1 second.
one complete revolution is equal to 360 degrees, so the ferris wheel is rotating 1/10 of 360 = 36 degrees every second.
now you want to make x represent time rather than degrees, so the function becomes:
y = 9.25 - 9.25 * cos(36x) + 3
x now represents time in seconds rather than angle in degrees.
after 1 second, the angle will be 36 degrees.
after 2 seconds, the angle will be 72 degrees.
etc.
the graph of that function is shown below:
see below the graph for further comments.

the first 2 graphs had their x-axis in terms of degrees starting from 0 degrees to 360 degrees.
the last graph had its x-axis in terms of seconds starting from 0 seconds to 10 seconds.
the function of y = 9.25 - 9.25 * cos(x) is where i started from.
x repr3esented number of degrees at that time.
how i figured it out is as follows:
at 0 degrees, the height of the car is equal to 0 feet in height.
this is before i added the 3 feet to adjust for the fact that at 0 degrees the car was actually 3 feet in height.
at 90 degrees, the height of the car is equal to 9.25 feet.
at 180 degrees, the height of the car is equal to 18.5 feet.
at 270 degrees, the height of the car is equal to 9.25 feet.
at 360 degrees, the height of the car is back to 0 feet again.
the following diagram shows that relationship.

the following diagram shows how the height of he ferris wheel was calculated.

|
|
|