To prove:


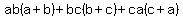 By Cauchy's inequality, the arithmetic mean of any number of
positive numbers is greater than or equal to the geometric mean.
Let's take two of the cubes to be the same.
The arithmetic mean of
By Cauchy's inequality, the arithmetic mean of any number of
positive numbers is greater than or equal to the geometric mean.
Let's take two of the cubes to be the same.
The arithmetic mean of  ,
, , and
, and  is greater
than or equal to the geometric mean of those cubes, two of which are the same.
is greater
than or equal to the geometric mean of those cubes, two of which are the same.


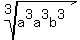






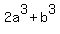

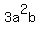 By symmetry we can also prove that
By symmetry we can also prove that
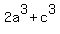




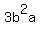


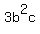
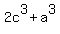

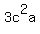
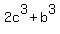

 Add all 6 inequalities:
Add all 6 inequalities:
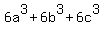

 Divide through by 3
Divide through by 3


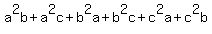 Factor out 2 on the left.
Rearrange the terms on the right so we can factor
pairwise and get the given desired right side:
Factor out 2 on the left.
Rearrange the terms on the right so we can factor
pairwise and get the given desired right side:


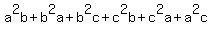 On the right, factor the 1st two, middle two and last two terms:
On the right, factor the 1st two, middle two and last two terms:


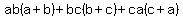 Edwin
Edwin