SOLUTION: A fair pair of dice is rolled 4 times. what is the probability of getting 7 twice?

Do you mean getting 7 AT LEAST twice or EXACTLY twice?

Either way we first get the probability of getting a seven 
with just ONE roll of the dice:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) 

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6) 

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) 

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) 

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 

That's 6 ways out of 36 or  or  as the probability
of getting seven out with just ONE roll.

To get exactly 2 seven rolls out of 4, we use the formula



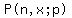
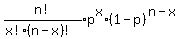with , , 



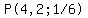
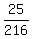
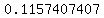That's the probability of getting exactly 2 sevens.

--------------------------------------------------------

To get the probability of 2 or more, calculate the probabilities of

exactly 3 and exactly 4 and add them to the above.

With a TI-83 or TI-84 calculator, binompdf( is for "exactly",
binomcdf( is for "exactly or fewer")

binompdf(4,1/6,2) under 2ND VARS

To get probability of 2 or more, 1 minus probability of 1 or fewer:

1-binomcdf(4,1/6,1)  get .1319444444 which is 

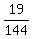Edwin