SOLUTION: A parabola has intercepts of x = -2, x = 3, and y = -4. a. Write the intercept form of the parabola. b. State the direction of the parabola. Explain. c. Write in ax2 +

Algebra ->  Quadratic Equations and Parabolas -> SOLUTION: A parabola has intercepts of x = -2, x = 3, and y = -4. a. Write the intercept form of the parabola. b. State the direction of the parabola. Explain. c. Write in ax2 +       Log On


   

Question 887945: A parabola has intercepts of x = -2, x = 3, and y = -4.
a. Write the intercept form of the parabola.
b. State the direction of the parabola. Explain.
c. Write in ax2 + bx + c form.
d. What is the axis of symmetry?
e. What is the vertex?
f. Graph the parabola. Label axis, vertex, and intercepts.

Someone please help this is soooooo confusing.
Found 2 solutions by josgarithmetic, Edwin McCravy:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Begin filling-in standard form equation. You know from those three points, a%3E0.
intercepts of x = -2, x = 3, and y = -4 means x for the vertex is %28-2%2B3%29%2F2=1%2F2.
y=a%28x-h%29%5E2%2Bk
What happens if solve for a?
a%28x-h%29%5E2=y-k
a=%28y-k%29%2F%28x-h%29%5E2
-
The two roots give+a=%28-k%29%2F%28-2-h%29%5E2 and a=%28-k%29%2F%283-h%29%5E2. Might be helpful now or maybe later.

We can also do this based on the two roots.
y=a%28x%2B2%29%28x-3%29
NOW try solving for a from this equation.
a=y%2F%28%28x%2B2%29%28x-3%29%29
Substitute for the y-intercept:
a=-4%2F%28%280%2B2%29%280-3%29%29
a=-4%2F%28-6%29
highlight_green%28a=2%2F3%29
Our equation can be stated, not standard form but as a factored form highlight%28y=%282%2F3%29%28x%2B2%29%28x-3%29%29.

We already saw what is x of the vertex and now we can find the y coordinate.
y=%282%2F3%29%281%2F2%2B2%29%281%2F2-3%29
%282%2F3%29%285%2F2%29%28-5%2F2%29=-%282%2A5%2A5%29%2F%283%2A2%2A2%29
highlight_green%28y=-25%2F6%29

Going back to finish standard form, highlight%28highlight%28y=%282%2F3%29%28x-1%2F2%29%5E2-25%2F6%29%29.

That should be sufficient for you to answer the other questions also.

Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
A parabola has intercepts of x = -2, x = 3, and y = -4.
Therefore it passes through the points (-2,0), (3,0), and (0,-4).

We plot those and sketch the graph approximately going through those
three points

a. Write the intercept form of the parabola.
x=-2 becomes x+2=0 and x=3 becomes x-3=0

The intercept form is 

y = a(x+2)(x-3)

because when you set that = 0 you get the x-intercepts x=-2 and x=3

b. State the direction of the parabola. Explain.
Looking at the graph above we can see that it can only open upward.

c. Write in ax2 + bx + c form.
We take the intercept form and substitute the y-intercept (0,-4)

 y = a(x+2)(x-3)
-4 = a(0+2)(0-3)
-4 = a(2)(-3)
-4 = -6a
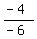%28-4%29%2F%28-6%29 = a
2%2F3 = a

[Note: We could have answered b above without looking at
the graph because if a is positive the graph opens
upward and if negative it opens downward]

Substitute for a:

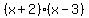 y = 2%2F3%28x%2B2%29%28x-3%29
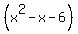 y = 2%2F3%28x%5E2-x-6%29
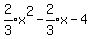
 y = expr%282%2F3%29x%5E2-expr%282%2F3%29x-4

e. What is the vertex?
We use the vertex formula:

The vertex is the point with x-coordinate -b%2F%282a%29 = 
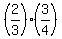
-%28-2%2F3%29%2F%282%282%2F3%29%29%22%22=%22%22%282%2F3%29%2F%284%2F3%29%22%22=%22%22%282%2F3%29%2A%283%2F4%29%22%22=%22%221%2F2

The y-coordinate of the vertex is found by substituting x=1%2F2 into the
original equation:

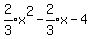 y = expr%282%2F3%29x%5E2-expr%282%2F3%29x-4
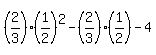 y = %282%2F3%29%281%2F2%29%5E2-%282%2F3%29%281%2F2%29-4
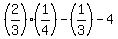 y = %282%2F3%29%281%2F4%29-%281%2F3%29-4
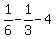 y = 1%2F6-1%2F3-4
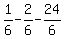 y = 1%2F6-2%2F6-24%2F6
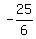 y = -25%2F6

So the vertex is %28matrix%281%2C3%2C1%2F2%2C%22%2C%22%2C-25%2F6%29%29, which is the
red point at the bottom of the graph below.

d. What is the axis of symmetry? 
The axis of symmetry is the vertical line whose equation is x=h, 
where h is the x-coordinate of the vertex. In this case it is x=1%2F2.
It is the vertical line passing through the vertex.

Axis of symmetry x=1%2F2, the green vertical line below:



Edwin